Malorientado escreveu:Sendo f(x)= 5-3x+2x², calcule f(A) onde A=[1 2/3 -4]. Coloquei as linhas da matriz A separadas por /.
Devo colocar 5 * In na resolução? Por que?
Note que f é uma função real. Ela recebe como entrada um número real e devolve como saída um outro número real. Mas A é uma matriz e não apenas um número real. Sendo assim, ao escrever f(A) não poderíamos simplesmente "substituir" x por A na função original devido ao número 5, pois ficaríamos com algo desse tipo: "5 - 3A + 2A²". E qual é o problema com essa expressão? Ora, A é uma matriz 2 por 2. Sendo assim, -3A e 2A² também serão matrizes 2 por 2. Mas o termo 5 é apenas um número. Sendo assim, ao escrever "5 - 3A + 2A²" você estaria dizendo para calcular a soma entre o número 5 e as matrizes -3A e 2A². Mas isso não faz sentido, pois o termo 5 também deveria ser uma matriz 2 por 2 para que a soma pudesse ser efetuada. Como contornar isso? Simples: por convenção "fingimos" que 5 é na verdade a matriz 5I, onde I é a matriz identidade de ordem 2 por 2.
Resumindo, para resolver o exercício basta efetuar a seguinte operação:
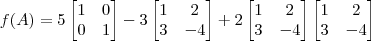
Agora tente continuar o exercício a partir daí.
ObservaçãoPor favor, procure usar o
LaTeX para digitar as notações de forma adequada.
Por exemplo, para digitar a matriz desejada basta usar o código:
- Código: Selecionar todos
[tex]
\begin{bmatrix}
1 & 2 \\
3 & -4
\end{bmatrix}
[/tex]
O resultado desse código será:
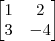



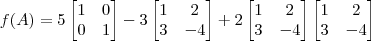
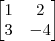


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
