 por iarapassos » Sáb Set 01, 2012 19:12
por iarapassos » Sáb Set 01, 2012 19:12
Olá pessoal.
O exercício do qual tenho dúvida é:
Determine, se possível, uma equação geral do plano determinado pelas retas r e s, nos seguintes casos:
c)

Eu fiz as questões a e b e nelas foi possível achar o vetor normal do plano formado pelas retas, pois eles eram LI e portanto paralelos. O produto vetorial dos vetores diretores das retas resulta na normal do plano.
Mas na letra c, os vetores são LD, ou seja, eles são paralelos. Nesse caso, como achar a equação geral do plano?
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Sáb Set 01, 2012 22:54
por LuizAquino » Sáb Set 01, 2012 22:54
iarapassos escreveu:O exercício do qual tenho dúvida é:
Determine, se possível, uma equação geral do plano determinado pelas retas r e s, nos seguintes casos:
c)

Eu fiz as questões a e b e nelas foi possível achar o vetor normal do plano formado pelas retas, pois eles eram LI e portanto paralelos. O produto vetorial dos vetores diretores das retas resulta na normal do plano.
Observação: o correto seria dizer "
achar o vetor normal do plano formado pelos vetores diretores das retas, pois eles eram LI e portanto não paralelos".
iarapassos escreveu:Mas na letra c, os vetores são LD, ou seja, eles são paralelos. Nesse caso, como achar a equação geral do plano?
Simples: como essas retas são paralelas e não coincidentes (verifique), basta escolher um ponto P na reta r e um ponto Q na reta s. Um vetor normal ao plano será dado por

(ou ainda, por
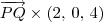
).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por iarapassos » Dom Set 02, 2012 22:15
por iarapassos » Dom Set 02, 2012 22:15
Verdade, acho que escrevei com pressa e acabei escrevendo errado. Se são LI, não são paralelos. E tbm mandei em falar "formado pelas retas" e não por seus vetores diretores. Valeu pela dica!
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [PLANO] Equação Geral
por manuel_pato1 » Sex Set 21, 2012 19:54
- 3 Respostas
- 2976 Exibições
- Última mensagem por manuel_pato1

Sáb Set 22, 2012 11:50
Geometria Analítica
-
- Equação geral do plano
por lucash96 » Seg Nov 02, 2015 16:51
- 0 Respostas
- 1302 Exibições
- Última mensagem por lucash96

Seg Nov 02, 2015 16:51
Geometria Analítica
-
- Encontrar a Equação Geral do Plano
por Vitor2+ » Seg Nov 14, 2011 02:21
- 7 Respostas
- 10640 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:04
Geometria Analítica
-
- Vértices do tetraedro e equação geral do plano
por -civil- » Qua Jun 15, 2011 23:04
- 1 Respostas
- 4015 Exibições
- Última mensagem por LuizAquino

Qui Jun 16, 2011 17:57
Geometria Analítica
-
- [Equação Plano] Transformar de geral pra paramétrica
por luankaique » Ter Ago 06, 2013 18:08
- 1 Respostas
- 4163 Exibições
- Última mensagem por Russman

Qua Ago 07, 2013 09:35
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 (ou ainda, por
(ou ainda, por 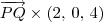 ).
).
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.