![log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
{2}^{\frac{7}{2}}-2 .2 log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
{2}^{\frac{7}{2}}-2 .2](/latexrender/pictures/2eb90ca51f78b6fa09d60e25e586c0b5.png)
olá ñ consegui saber oq faço com esse -2 antes da multiplicação,ele parece ñ se encaixar em nenhuma das propriedades de logarítimos!
A resposta do gabarito é -1/2
Por acaso existe subtração de númros de mesma base com expoentes diferentes?

![log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
{2}^{\frac{7}{2}}-2 .2 log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
{2}^{\frac{7}{2}}-2 .2](/latexrender/pictures/2eb90ca51f78b6fa09d60e25e586c0b5.png)



Adilson escreveu:
olá ñ consegui saber oq faço com esse -2 antes da multiplicação,ele parece ñ se encaixar em nenhuma das propriedades de logarítimos!
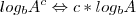


![log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
log{2}^{{2}^{3}}\sqrt[]{2}-2.log{2}^{log{3}^{{3}^{4}}} log{2}^{8\sqrt[]{2}}-2 .log{2}^{log{3}^{81}}
log{2}^{{2}^{3}}\sqrt[]{2}-2.log{2}^{log{3}^{{3}^{4}}}](/latexrender/pictures/05bbd27a1b31965b8a35c00a9e70b74e.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)