 por samra » Dom Ago 19, 2012 18:37
por samra » Dom Ago 19, 2012 18:37
Olá, alguém me ajuda resolver essa questao. por favor. (Usando L'hospital)
indeterminação do tipo

-

A resposta é 1/2, a minha está dando 0

Eu igualei os denominadores e apliquei L'hopital , derivando o numerador e o denominador (logicamente sem usar a regra da derivada para quociente).
Alguém me ajuda a visualizar onde errei?
att. Sammy
Ps.: limite em anexo
- Anexos
-

"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por e8group » Dom Ago 19, 2012 19:58
por e8group » Dom Ago 19, 2012 19:58
Note que ,
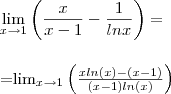
.
Agora temos uma indeterminação 0/0 mas derivando teremos outra indeterminação 0/0 , ou seja vamos aplicar" L'hospital " duas vezes assim segue ,
![\lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ] \lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ]](/latexrender/pictures/0caee27a19890c2a06dcae6fdb4fe3dc.png)
.Assim , obtemos :

Qualquer dúvida comente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1916 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 21:16
- 9 Respostas
- 3349 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 16, 2011 15:20
Cálculo: Limites, Derivadas e Integrais
-
- regra de L' Hospital
por matmatco » Qua Nov 30, 2011 13:47
- 5 Respostas
- 2477 Exibições
- Última mensagem por matmatco

Sáb Dez 03, 2011 07:10
Cálculo: Limites, Derivadas e Integrais
-
- Derivada regra de L'Hospital
por Wumaxeb » Sex Mai 27, 2011 22:19
- 2 Respostas
- 3106 Exibições
- Última mensagem por Molina

Sex Mai 27, 2011 23:24
Cálculo: Limites, Derivadas e Integrais
-
- [Regra de L'Hospital] Indeterminções
por erickm93 » Seg Jun 24, 2013 11:47
- 1 Respostas
- 1645 Exibições
- Última mensagem por Man Utd

Qui Jun 27, 2013 11:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 -
- 



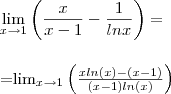 .
.![\lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ] \lim_{x\to 1}\left(\frac{x ln(x) - (x-1)}{(x-1)ln(x)} \right) = \lim_{x\to1} \left[\frac{\mathrm{d^2} }{\mathrm{d} x^2}\left( \frac{x ln(x) - (x-1)}{(x- 1)ln(x)}\right ) \right ]](/latexrender/pictures/0caee27a19890c2a06dcae6fdb4fe3dc.png) .Assim , obtemos :
.Assim , obtemos :


 .
.
 :
: