 por anfran1 » Dom Ago 19, 2012 15:28
por anfran1 » Dom Ago 19, 2012 15:28
Fiz hoje a prova e tinha um exercício que eu não consegui resolver. Se alguém souber por favor me explique.
Prove que

para qualquer número natural.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Ago 19, 2012 17:31
por MarceloFantini » Dom Ago 19, 2012 17:31
Você já aprendeu sobre o
Princípio da Indução Finita? Isto resolve a questão. Se souber, é simples, se não veja e conseguirá resolver.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anfran1 » Dom Ago 19, 2012 17:39
por anfran1 » Dom Ago 19, 2012 17:39
Sim eu tenho que colocar o K+1 e ver se é verdadeira.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anfran1 » Seg Ago 20, 2012 20:24
por anfran1 » Seg Ago 20, 2012 20:24
O que eu faço depois de:

?
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Ago 20, 2012 21:01
por MarceloFantini » Seg Ago 20, 2012 21:01
Você tem que expandir
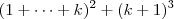
e chegar em
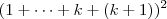
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por anfran1 » Ter Ago 21, 2012 13:38
por anfran1 » Ter Ago 21, 2012 13:38
MarceloFantini escreveu:Você tem que expandir
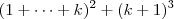
e chegar em
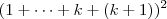
.
Isso eu sei mas não consigo chegar na equação.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anfran1 » Dom Ago 26, 2012 10:17
por anfran1 » Dom Ago 26, 2012 10:17
Por favor eu já expandi mas não consigo chegar em

. O que está me complicando é essa parte das reticências. Alguém poderia me ajudar?
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anfran1 » Qui Ago 30, 2012 20:45
por anfran1 » Qui Ago 30, 2012 20:45
Essa questão já está me incomodando um pouco. Como faço para expandir
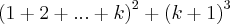
para chegar em
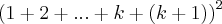
?
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Ago 30, 2012 22:10
por fraol » Qui Ago 30, 2012 22:10
Boa noite,
Sabendo que
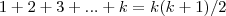
( a soma dos k termos de uma PA com
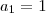
e razão

),
Tem-se então que

Agora vamos desenvolver:
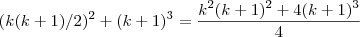
=

=
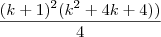
=

=
![\left[ \frac{(k+1)(k + 2)}{2}\right]^2 \left[ \frac{(k+1)(k + 2)}{2}\right]^2](/latexrender/pictures/dc55c83130659bab8d16eb68d2111073.png)
(que é o quadrado da soma dos

termos de uma uma PA com
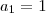
e razão

)
=

.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por anfran1 » Sex Ago 31, 2012 17:13
por anfran1 » Sex Ago 31, 2012 17:13
Nossa não pensei nessa PA. Muito obrigado.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números naturais
por jose henrique » Dom Ago 15, 2010 15:24
- 2 Respostas
- 1705 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 10:40
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 11:44
- 0 Respostas
- 1176 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 11:44
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 12:31
- 1 Respostas
- 1628 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:06
Álgebra Elementar
-
- números naturais
por jose henrique » Ter Ago 24, 2010 23:49
- 3 Respostas
- 2192 Exibições
- Última mensagem por MarceloFantini

Qua Ago 25, 2010 13:13
Álgebra Elementar
-
- Conjunto dos números naturais
por adriano rodrigues » Dom Dez 12, 2010 18:24
- 3 Respostas
- 3181 Exibições
- Última mensagem por adriano rodrigues

Ter Dez 14, 2010 19:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para qualquer número natural.
para qualquer número natural.
 para qualquer número natural.
para qualquer número natural.



 ?
?

e chegar em
.

 . O que está me complicando é essa parte das reticências. Alguém poderia me ajudar?
. O que está me complicando é essa parte das reticências. Alguém poderia me ajudar?
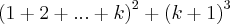 para chegar em
para chegar em 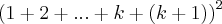 ?
?
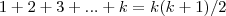 ( a soma dos k termos de uma PA com
( a soma dos k termos de uma PA com 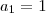 e razão
e razão  ),
),
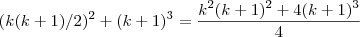

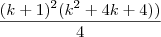

![\left[ \frac{(k+1)(k + 2)}{2}\right]^2 \left[ \frac{(k+1)(k + 2)}{2}\right]^2](/latexrender/pictures/dc55c83130659bab8d16eb68d2111073.png)
 termos de uma uma PA com
termos de uma uma PA com 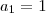 e razão
e razão  )
)


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.