 por Danilo » Ter Ago 14, 2012 15:32
por Danilo » Ter Ago 14, 2012 15:32
Simplificar,
![{\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}} {\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}}](/latexrender/pictures/0baf758613a268f110b58575cc00cc83.png)
eu fiz assim:
=
![\sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}} \sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}}](/latexrender/pictures/6cd1ae76fedd5c7c40f0229a913b66be.png)
=
![\sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)} \sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)}](/latexrender/pictures/445daf25303e4fb18acb8b8b51047fae.png)
=
![\sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}}](/latexrender/pictures/55f0ecbf13937f192e4053fa62ba2b22.png)
=
![\sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}}](/latexrender/pictures/ef26b01bd67a48007f69c9f7e6368b6f.png)
=
![\sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}} \sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}}](/latexrender/pictures/b520bc662c38aec1789dffebe35c447e.png)
e é aqui que eu não sei mais o que fazer... a resposta é
![\sqrt[]{a} + \sqrt[]{b} \sqrt[]{a} + \sqrt[]{b}](/latexrender/pictures/2e9c7b25c2340c81571cc55454c06f8c.png)
.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Ter Ago 14, 2012 17:09
por e8group » Ter Ago 14, 2012 17:09
Observe que sua expressão se resume a isto ,

.Agora seja ,

.Assumindo

e

são números positivos ,temos :

.
Fazendo ,
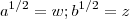
segue que :
![x^2 =\frac{ w^3 + z^3 +3(wz)[w+z]}{w+z} x^2 =\frac{ w^3 + z^3 +3(wz)[w+z]}{w+z}](/latexrender/pictures/d1d12061d33ea6768575f02817ef5871.png)
.Logo ,
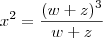
.Ou seja ,

,lembrando que

.Assim concluímos que ,
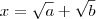
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Danilo » Qua Ago 15, 2012 02:38
por Danilo » Qua Ago 15, 2012 02:38
Valeu !

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificar
por Sandy26 » Ter Abr 27, 2010 14:35
- 5 Respostas
- 3166 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 18:29
Cálculo: Limites, Derivadas e Integrais
-
- Simplificar
por victorleme » Qua Mai 04, 2011 20:06
- 4 Respostas
- 2516 Exibições
- Última mensagem por victorleme

Qui Mai 05, 2011 18:56
Polinômios
-
- Simplificar
por mayconf » Sáb Set 22, 2012 14:02
- 4 Respostas
- 2259 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 17:57
Álgebra Linear
-
- Simplificar
por Thyago Quimica » Qui Mar 20, 2014 17:52
- 1 Respostas
- 1230 Exibições
- Última mensagem por natomi

Qui Mar 20, 2014 17:57
Funções
-
- simplificar equação
por sinuca147 » Qui Mai 21, 2009 03:11
- 2 Respostas
- 6974 Exibições
- Última mensagem por sinuca147

Qui Mai 21, 2009 15:12
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}} {\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}}](/latexrender/pictures/0baf758613a268f110b58575cc00cc83.png)
![\sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}} \sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}}](/latexrender/pictures/6cd1ae76fedd5c7c40f0229a913b66be.png) =
= ![\sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)} \sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)}](/latexrender/pictures/445daf25303e4fb18acb8b8b51047fae.png) =
= ![\sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}}](/latexrender/pictures/55f0ecbf13937f192e4053fa62ba2b22.png) =
= ![\sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}}](/latexrender/pictures/ef26b01bd67a48007f69c9f7e6368b6f.png) =
= ![\sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}} \sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}}](/latexrender/pictures/b520bc662c38aec1789dffebe35c447e.png)
![\sqrt[]{a} + \sqrt[]{b} \sqrt[]{a} + \sqrt[]{b}](/latexrender/pictures/2e9c7b25c2340c81571cc55454c06f8c.png) .
.
![{\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}} {\left[\left(a\sqrt[]{a} + b\sqrt[]{b} \right){ \left(\sqrt[]{a} + \sqrt[]{b} \right)}^{-1} + 3\sqrt[]{ab} \right]}^{\frac{1}{2}}](/latexrender/pictures/0baf758613a268f110b58575cc00cc83.png)
![\sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}} \sqrt[]{\frac{a\sqrt[]{a} + b\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} + 3\sqrt[]{ab}}](/latexrender/pictures/6cd1ae76fedd5c7c40f0229a913b66be.png) =
= ![\sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)} \sqrt[]{\left(\frac{a\sqrt[]{a} + b\sqrt[]{b} + 3a\sqrt[]{b} + 3b\sqrt[]{a}}{\sqrt[]{a} + \sqrt[]{b}} \right) \cdot \left(\frac{\sqrt[]{a} - \sqrt[]{b}}{\sqrt[]{a} - \sqrt[]{b}} \right)}](/latexrender/pictures/445daf25303e4fb18acb8b8b51047fae.png) =
= ![\sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{{a}^{2} + b\sqrt[]{ab} + 3a\sqrt[]{ab} + 3ab - a\sqrt[]{ab} - {b}^{2} - 3ab -3b\sqrt[]{ab}}{a-b}}](/latexrender/pictures/55f0ecbf13937f192e4053fa62ba2b22.png) =
= ![\sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}} \sqrt[]{\frac{\left(a+b \right)\left(a-b \right)-2b\sqrt[]{ab} + 2a\sqrt[]{ab}}{a-b}}](/latexrender/pictures/ef26b01bd67a48007f69c9f7e6368b6f.png) =
= ![\sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}} \sqrt[]{\frac{\left(a+b \right) -2\sqrt[]{ab}\left(b-a \right)}{a-b}}](/latexrender/pictures/b520bc662c38aec1789dffebe35c447e.png)
![\sqrt[]{a} + \sqrt[]{b} \sqrt[]{a} + \sqrt[]{b}](/latexrender/pictures/2e9c7b25c2340c81571cc55454c06f8c.png) .
.
 .Agora seja ,
.Agora seja , .Assumindo
.Assumindo  e
e  são números positivos ,temos :
são números positivos ,temos : .
.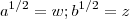 segue que :
segue que :![x^2 =\frac{ w^3 + z^3 +3(wz)[w+z]}{w+z} x^2 =\frac{ w^3 + z^3 +3(wz)[w+z]}{w+z}](/latexrender/pictures/d1d12061d33ea6768575f02817ef5871.png) .Logo ,
.Logo ,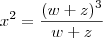 .Ou seja ,
.Ou seja ,  ,lembrando que
,lembrando que  .Assim concluímos que ,
.Assim concluímos que ,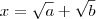 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

