 por Danilo » Ter Ago 14, 2012 00:52
por Danilo » Ter Ago 14, 2012 00:52
Não estou conseguindo simplificar uma expressão...
![\frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right] \frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right]](/latexrender/pictures/a12db7aad1d0d1de141afe911f6f4e8f.png)
tentei fazer assim:

![\frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right) \frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right)](/latexrender/pictures/cfd64f0ae2b92367b758c9581fae56c3.png)
racionalizando,
![\frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right) \frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right)](/latexrender/pictures/48b2f3cc54195f65ebdff46da8b0a6de.png)
e é aqui que eu travo. Dá uma conta chata mas eu não consigo chegar no resultado, que é -1.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Ter Ago 14, 2012 01:10
por MarceloFantini » Ter Ago 14, 2012 01:10
Você errou algumas contas:
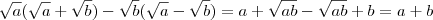
. Daí,
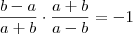
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Ter Ago 14, 2012 01:25
por Danilo » Ter Ago 14, 2012 01:25
MarceloFantini escreveu:Você errou algumas contas:
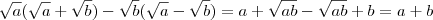
. Daí,
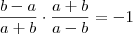
.
tudo por um sinal... valeu

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em expressão
por ginrj » Sex Mar 06, 2009 18:45
- 2 Respostas
- 4216 Exibições
- Última mensagem por ginrj

Sáb Mar 07, 2009 12:01
Álgebra Elementar
-
- Expressão duvida !!!
por LuizCarlos » Qui Ago 11, 2011 14:57
- 1 Respostas
- 1639 Exibições
- Última mensagem por Molina

Qui Ago 11, 2011 16:40
Álgebra Elementar
-
- Dúvida sobre ''sinal da expressão ax+b''
por Danilo » Dom Abr 22, 2012 03:41
- 5 Respostas
- 2953 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:20
Álgebra Elementar
-
- [Expressão Númerica] Dúvida ambigua
por umbrorz » Qui Mai 10, 2012 15:23
- 2 Respostas
- 2094 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:06
Funções
-
- Dúvida exercício expressão logaritima
por kalanicastanho » Seg Mai 30, 2016 09:30
- 1 Respostas
- 3377 Exibições
- Última mensagem por nakagumahissao

Seg Mai 30, 2016 23:10
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right] \frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right]](/latexrender/pictures/a12db7aad1d0d1de141afe911f6f4e8f.png)

![\frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right) \frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right)](/latexrender/pictures/cfd64f0ae2b92367b758c9581fae56c3.png)
![\frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right) \frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right)](/latexrender/pictures/48b2f3cc54195f65ebdff46da8b0a6de.png)

![\frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right] \frac{b-a}{a+b} \cdot \left[{a}^{\frac{1}{2}} \cdot {\left({a}^{\frac{1}{2}} - {b}^{\frac{1}{2}} \right)}^{-1} - {\left(\frac{{a}^{\frac{1}{2}} + {b}^{\frac{1}{2}}}{{b}^{\frac{1}{2}}} \right)}^{-1} \right]](/latexrender/pictures/a12db7aad1d0d1de141afe911f6f4e8f.png)

![\frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right) \frac{b-a}{a+b} \left(\frac{\sqrt[]{a}}{\sqrt[]{a} - \sqrt[]{b}} - \frac{\sqrt[]{b}}{\sqrt[]{a} + \sqrt[]{b}} \right)](/latexrender/pictures/cfd64f0ae2b92367b758c9581fae56c3.png)
![\frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right) \frac{b-a}{a+b} \left(\frac{a + 2\sqrt[]{ab} - b}{a - b} \right)](/latexrender/pictures/48b2f3cc54195f65ebdff46da8b0a6de.png)


. Daí,
.




 .
.
 :
: