Considere a seguinte figura que mostra uma sequência de quadrados, em que o lado L do primeiro é o dobro do lado do segundo; o lado do segundo é o dobro do lado do terceiro e assim indefinidamente.
Esses quadrados representam as bases de caixas retangulares, todas com 1 m de altura.
Nessas condições, é CORRETO afirmar que a soma S dos volumes de todas essas infinitas caixas é
A) infinita.
B) um número finito, porém muito grande.
C) um número entre 2L2 e 3L2.
D) um número entre L2 e 2L2.




 -ésima caixa é dado por
-ésima caixa é dado por .
. temos
temos  . Para
. Para  , temos
, temos  . Para
. Para  , temos
, temos  . Assim, sucessivamente. Portanto, podemos supor que
. Assim, sucessivamente. Portanto, podemos supor que 
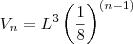 .
. e primeiro termo
e primeiro termo  . Logo, efetuando a soma infinita de seus termos, obtemos
. Logo, efetuando a soma infinita de seus termos, obtemos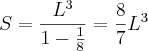 .
.

 .
.
 :
: