Sou estudante de Eng. Elétrica e estou tentando modelar matematicamente um tanque que estou desenvolvendo para a disciplina de Controle. Eu até entendo, razoavelmente da teoria de controle mas estou me batendo na matemática do tanque, se fossem circuitos eu acho que conseguiria modelar com mais tranquilidade...
Bom,
minha dúvida é a seguinte.
Calculei o volume do tronco do cone circular (de dimensões ainda desconhecidas) utilizando o princípio da integral de revolução.
E obtive:
![V = (pi/3)*(hmax/(r2-r1))*[r2(t)^3-r1^3] V = (pi/3)*(hmax/(r2-r1))*[r2(t)^3-r1^3]](/latexrender/pictures/530a6fb11074bd55682b8fe96afd4a83.png)
Sendo
 - volume do líquido contido no tronco do cone
- volume do líquido contido no tronco do cone - altura máxima do tronco do cone
- altura máxima do tronco do cone - maior raio do cone (topo)
- maior raio do cone (topo) - menor raio do cone(base)
- menor raio do cone(base)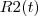 - raio do círculo formado pelo líquido em uma altura qualquer do cone
- raio do círculo formado pelo líquido em uma altura qualquer do coneNessa parte fiz alguns testes e acredito que esteja correto.
Mas o problema é que vou controlar a altura da coluna de líquido
 , assim, não posso depender do raio
, assim, não posso depender do raio 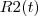 .
.Logo, preciso achar uma relação para eu substituir o
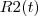 por
por  .
.Sendo
 a altura do líquido em um instante qualquer.
a altura do líquido em um instante qualquer.Como eu ainda vou construir o tanque(nesse formato), ainda não posso determinar as dimensões do tronco do cone, ou seja, não sei qual a abertura do cone... (motivo o qual eu inclui
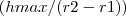 no cálculo do volume, se for um cone circular reto
no cálculo do volume, se for um cone circular reto 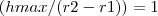
Já estou quebrando a cabeça com isso tem alguns dias...
Obrigado pessoal!
Abraços


