Numa brincadeira, Mateus posiciona a bola a 4 m da rede e Lucas varia sua posição em lado oposto à rede, aproximando-se ou afastando-se dela, conservando uma mesma linha reta coma bola, perpendicular à rede.
Mateus lança a bola para Lucas co um único toque na bola, sem que atinja o chão, sem tocar a rede.
Considere um plano cartesiano em que:
- cada lançamento realizado por Mateus é descrito uma trajetória parabólica;
- Lucas e o ponto de partida da bola estão no eixo
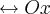(A SETA É EM CIMA DO Ox) - a posição da bola é um ponto (x,y) desse plano, onde y=f(x) é a altura atingida pela bola, em metros, em relação ao chão.
Assinale, dentre as alternativas abaixo, aquela que tem a lei de uma função f que satisfaz às condições estabelecidas na brincadeira de Lucas e Mateus.
a) f(x) = - x²/8 + 2 b) -x²/16 + x/4+15/4
c) f(x)= -3x²/16 + 3 d) -0,1x² + 0,2x + 4,8
Veja se estou correto para fazer recurso?
Resolução: ANULADA
Sem perda de generalidade, considere que Mateus está situado num ponto x m= que é a menor raiz da
parábola descrita pela bola. Para que encontremos uma equação de parábola que satisfaça as informações
do problema, o valor numérico para x m= + 4 deve ser no mínimo igual a 3, de forma que a bola
ultrapasse a rede.Como não foi dito em que posição está a origem do sistema de eixos, qualquer parábola que atenda à
condição supracitada satisfaz ao problema. Portanto, a única equação que NÃO satisfaz ao problema é f(x)= -x²/8 + 2.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.