![\sqrt[2]{3x+a²+3a} \sqrt[2]{3x+a²+3a}](/latexrender/pictures/aaf671fa05fb55f2169aab7fb7538224.png) , em que x é a incógnita e a
, em que x é a incógnita e a  IR tal que a<-3, possui conjunto solução S, S
IR tal que a<-3, possui conjunto solução S, S IR.
IR.Sobre S tem-se as seguintes proposições.
I) Possui exatamente dois elementos.
II) Não possui elemento menor que 2.
III) Possui elemento maior que 3.
Sobre as proposições acima, são verdadeiras.
a) apenas I e II c) apenas II e III
b) apenas I e III d) I, II e III
No gabarito ta c mas eu achei b
Veja se eu estou certo !
x=
![\sqrt[2]{3x+a²+3a} \sqrt[2]{3x+a²+3a}](/latexrender/pictures/aaf671fa05fb55f2169aab7fb7538224.png) é uma raiz, logo x ? 0 . Elevando ao quadrado:
é uma raiz, logo x ? 0 . Elevando ao quadrado:x² ? 3x ? a(a + 3) = 0 ? x = ?a ou x = a + 3 . Substituindo a por valores possíveis que é a<-3
(I) Possui exatamente dois elementos (V)
(II) Não possui elemento menor que 2. (F)
(III) Possui elemento maior que 3. (V)


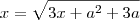

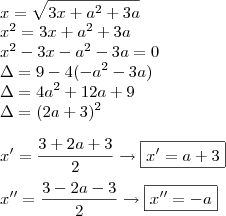
 , mas, devemos fazer a verificação.
, mas, devemos fazer a verificação.
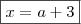 , sabemos que
, sabemos que 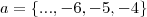 , então
, então 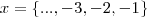 .
. e
e  na equação inicial
na equação inicial 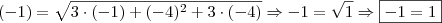
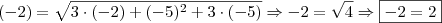

 , como
, como 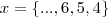 .
.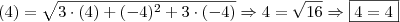


 .
. ,
,  e para
e para  ,
,  .
.
 , monte a função e substitua
, monte a função e substitua  .
.
