


 %
%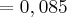 .
.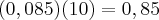


gouveia escreveu:Tem certeza? Fiquei intrigado porque este seria o intuitivo, mas se for assim, significa que caso me espusesse a 20 sorteios teria uma chance de 170%. E após duas tentativas na moeda a minha chance de tirar coroa seria de 100%?



Cleyson007 escreveu:Bom dia Gouveia!
Primeiramente, seja bem vindo ao Ajuda Matemática!
Gouveia, vou tentar resolver sua questão..
Como você mesmo diz: "pergunta simples"..
Essas questões que se apresentam simples demais, costumam esconder pegadinhas..
Acho que seria isso: Chance em um sorteio:%
.
Como são 10 sorteios, a chance é multiplicada em cada sorteio:
Logo a chance de ser aprovado seria de 85%.
Até mais.
Um abraço.

 --->
---> =>
=>

gouveia escreveu:Grato pela formula , mas fiz uma simulação com valores mais altos e o resultado acaba por reduzir a probabilidade o que é um contra senso. Faz uma tentativa com 20 por exemplo
Abs


Brown escreveu:Uma pessoa gastou 2/7 do que possuia e depois gastou 1/3 do que sobrou ficando ainda com 300.00


Felipe Schucman escreveu:gouveia escreveu:Grato pela formula , mas fiz uma simulação com valores mais altos e o resultado acaba por reduzir a probabilidade o que é um contra senso. Faz uma tentativa com 20 por exemplo
Abs
Na verdade seria um contra senso se dissemos que a probabilidade de ganhar diminuiu, mas na verdade dizermos que a probabilidade de ganhar apenas uma vez diminui, isso porque a probabilidade de ganhar mais vezes pode não ter diminuido, alias pode ter aumentando a probabilidade de ganhar 2, 3 ou mais vezes... Essa distribuição te diz a probabilidade de ganhar APENAS 1 vez...mas você pode a calcular a probabilidade de ganhar as 10 de 10 sorteios....caso queira uma forma melhor de calcular descreve melhor a situação.
Um Abraço!




gouveia escreveu:Felipe Schucman escreveu:Então, vou explicar novamente....essa distribuição que mostrei, calcula a probabilidade de ganhar k vezes, um numero que você escolhe...se você colocar 1, calculará a probabilidade de você ganhar uma vezes. O que ocorre é, quando você aumenta o numero de vezes que se joga, para 20 no caso, a probabilidade de ganhar k > 1< 20(sendo k inteiro) aumenta, então como a probabilidade de ganhar mais de uma vez aumenta a probabilidade de ganhar APENAS uma vez diminui.
Se você tiver a necessecidade de um outro calculo, me relate melhor a sensação que tento encaixar o caso em uma outro distribuição de probabilidade. Pois o que ocorre nessa distribuição que lhe passei é que mesmo que a vitória ocorra na terceira tentativa, por exemplo, as outras vezes você ainda jogará pondendo ou não ganhar novamente.
Espero que não tenha ficado confuso!
Um Abraço



gouveia escreveu:Li seu post acima com atraso. Neste caso vc conhece uma formula que indique a probabilidade de ganhar AO MENOS uma vez, nao interessando se vai ganhar apenas uma vez, ou 2 vezes, 3 vezes, etc.....
Abs e obrigado pela atencao



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.