hygorvv escreveu:Obtenha equações do lugar geométrico dos pontos médios dos segmentos que se apoiam nas retas r e s e interprete geometricamente, no caso em que:
r: X=(1,2,2)+

(0,1,1) e s: X=(0,0,0)+
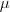
(1,0,1).
Resposta: 2x+2y-2z-1=0
Galera, interpretar geometricamente eu até consigo, não consigo é obter os pontos médios para tentar tirar alguma conclusão.
Cada segmento "se apoia" nas retas r e s. Em outras palavras, cada segmento tem um dos extremo na reta r e o outro na reta s.
Sejam P e Q os extremos de um segmento qualquer, de tal modo que P está em r e Q está em s.
Como P está em r, existe um escalar a tal que P = (1, 2, 2) + a(0, 1, 1). Por outro lado, como Q está em s, existe um escalar b tal que Q = (0, 0, 0) + b(1, 0, 1).
Desse modo, o ponto médio entre P e Q será dado por:
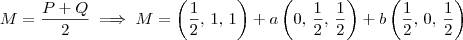
Agora tente continuar a partir daí.
 (0,1,1) e s: X=(0,0,0)+
(0,1,1) e s: X=(0,0,0)+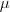 (1,0,1).
(1,0,1).

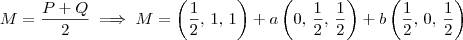



 , avisa que eu resolvo.
, avisa que eu resolvo.

