


CarolMarques escreveu:Decomponha u =(1,0,3) como soma dos vetores v e w tais que v, (1,1,1) e (-1,1,2) sejam LD e w seja ortogonal aos dois últimos.
CarolMarques escreveu:Não sei como fazer essa questão por favor me ajudem.
 seja L.D., basta que existam escalares a e b tais que:
seja L.D., basta que existam escalares a e b tais que:
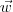 deve ser ortogonal a (1, 1, 1) e (-1, 1, 2), uma possibilidade é tomar
deve ser ortogonal a (1, 1, 1) e (-1, 1, 2), uma possibilidade é tomar  . Calculando esse produto vetorial, obtemos que
. Calculando esse produto vetorial, obtemos que 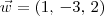 .
.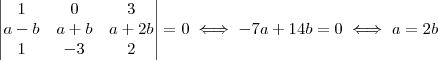
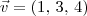 .
.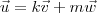 . Em outras palavras, basta resolver a equação:
. Em outras palavras, basta resolver a equação: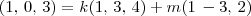

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.