Carl Friedrich Gauss (1777 – 1855) foi o matemático com maior destaque no século XIX.
Dentre inúmeras contribuições de Gauss à Matemática, ele é considerado um dos
primeiros matemáticos a associar números complexos a pares ordenados de números
reais. (RIBEIRO, 2010. p. 278).
Três números complexos z1, z2 e z3 são tais que |z1 – z2| = 7, |z2 – z3| = 8 e |z3 – z1| = 9.
Sendo A, B e C os afixos desses números, no plano de Argand-Gauss, pode-se afirmar que a medida,
em u.c. do raio da circunferência inscrita no triângulo ABC, é igual a:


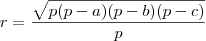 , onde:
, onde:  é o raio da circunferência inscrita.
é o raio da circunferência inscrita.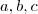 são os lados do triângulo.
são os lados do triângulo.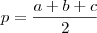 (semiperímetro do triângulo).
(semiperímetro do triângulo).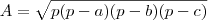 ) e no cálculo da área do triângulo em função do raio da circunferência inscrita (
) e no cálculo da área do triângulo em função do raio da circunferência inscrita (  ).
).
 ,entretanto por outro lado obtemos :
,entretanto por outro lado obtemos :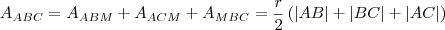
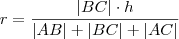 .Lembrando que
.Lembrando que 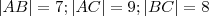 implica
implica 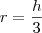

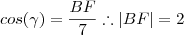 e finalmente
e finalmente  .Ou seja ,
.Ou seja ,

 .
.
 :
: