Boa noite a todos,
Gostaria de saber, se possível, se estes exercícios que resolvi e entreguei a uma professora minha, merecem a nota que ela me deu.
Resolvi os exercícios com um colega meu e ele acabou por ter 16 valores e eu apenas tive 5 valores.
Não acho justo que, alguns professores, seja por falta de carácter, seja por terem embirrado connosco, nos possam dar uma nota destas.
Peço que apenas me digam se realmente a resolução destes exercícios merece a nota de 5 valores, porque tenho a noção do que fiz, e não penso que mereça menos de 12 ou 13 valores.
O comentário da professora foi o seguinte: "Infelizmente o seu trabalho não chega para passar. Com um trabalho de avaliação feito em casa, não se compreende que tenha errado nas definições."
Cada alínea vale 3 valores, excepto a 2 a), que vale 2 valores.
Obrigado.
http://imageshack.us/photo/my-images/843/99832567.jpg/
http://imageshack.us/photo/my-images/821/20324985.jpg/
http://imageshack.us/photo/my-images/411/32557063.jpg/
http://imageshack.us/photo/my-images/694/73911528.jpg/




 um Espaço Vectorial e sejam
um Espaço Vectorial e sejam  ,
,  ,
,  ,
,  ,
,  e u vectores de
e u vectores de  espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que:
espaços vectoriais sobre o corpo K e ?:V?U uma aplicação linear. Mostrar que: ) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?(
) é um sistema de vectores linearmente dependente, então o mesmo acontece com o sistema (?( ,
, ,
, ,
, ,
,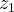 e
e 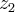 ?K
?K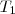 =?
=?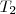 =?
=?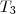 =?
=?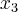 ,
, e
e  ? K.
? K. +
+ +
+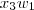 +
+ +
+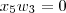
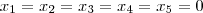 , ou seja, que a única combinação linear é a trivial.
, ou seja, que a única combinação linear é a trivial. <=>
<=> 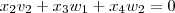 também é linearmente independente.
também é linearmente independente.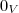 .
. v?F?V,
v?F?V, ?K
?K
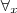 ?K.
?K.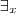 ?F tal que:
?F tal que: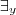 ??(F) tal que:
??(F) tal que: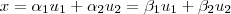 , com
, com  . Então
. Então 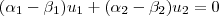 mas os coeficientes são não-nulos e assim
mas os coeficientes são não-nulos e assim  não seria base.
não seria base.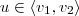 . Então existem coeficientes
. Então existem coeficientes  tais que
tais que  . Como
. Como 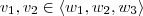 , então
, então  . Mas daí
. Mas daí
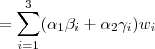 ,
,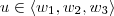 .
.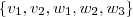 é linearmente independente, então vale a condição
é linearmente independente, então vale a condição 

 então
então  também é um espaço vetorial, cujo único elemento é o elemento neutro. Se
também é um espaço vetorial, cujo único elemento é o elemento neutro. Se  são subspaços vetoriais de
são subspaços vetoriais de  .
. são linearmente dependentes, então existem constantes
são linearmente dependentes, então existem constantes  nem todas nulas, tais que
nem todas nulas, tais que  . Usando a aplicação linear nesta combinação, temos
. Usando a aplicação linear nesta combinação, temos ,
, igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente.
igual a zero sendo que nem todos os coeficientes são nulos, portanto é linearmente dependente. , então
, então 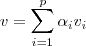 . Daí,
. Daí, 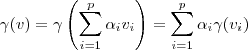
 . Como
. Como 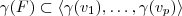 , segue
, segue 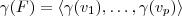 .
.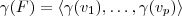 . É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.
. É isto que você quer provar, é sua tese, não sua hipótese. Afirmando esta igualdade, não há nada para provar; se é o espaço gerado, é óbvio que qualquer vetor é escrito como combinação linear destes.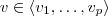 com
com 
 é injetiva, então segue que
é injetiva, então segue que 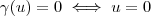 . Aplicando nesta combinação, temos
. Aplicando nesta combinação, temos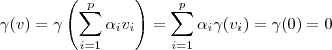 .
. e disso
e disso 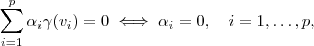 mostrando que o conjunto de vetores
mostrando que o conjunto de vetores 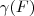 .
.