Eu estava pensando... da potênciação surge a função exponencial (resultado em função do expoente) e a sua inversa, a função logarítmca (expoente em função do resultado), mas e da radiciação, não surge nenhuma função?
Não conheço nenhuma, então fiz o gráfico do resultado em função do índice da raiz de e o gráfico do índice da raiz de e em função do resultado dela.
Vejam a cara delas: (g(x) é a inversa de f(x))

e aqui, em vez de usar o radicando e, usei o radicando 10 (q(x) é a inversa de p(x))

observem que eu usei a propriedade logaritímica de mudança de base na função q(x).
acho que a propriedade diferencial de que a derivada de e^x é e^x e de que a derivada de ln x é ln x, afinal de contas, usei o conceito de função exponencial e logaritimica na base e para demonstrar minha "descoberta" eiaheiaeiauhe
alguém sabe algo a respeito?? consegue ver alguma utilidade nisso? kkkk


 pois esta é solução de uma série de equações cheias de aplicações Física, Econômicas, Probabilísticas e muitas outras.
pois esta é solução de uma série de equações cheias de aplicações Física, Econômicas, Probabilísticas e muitas outras. .
.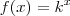
 .
.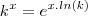 ,
,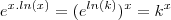 ,
, .
. mas uma FUNÇÃO REAL
mas uma FUNÇÃO REAL  , então
, então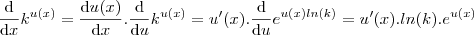 .
.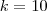 e
e  obteremos os seus resultados.
obteremos os seus resultados.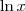 é
é  , não o próprio logaritmo. A função inversa da raíz enésima é a enésima potência.
, não o próprio logaritmo. A função inversa da raíz enésima é a enésima potência.

 . Desenhe e veja.
. Desenhe e veja.