Estou com problemas para visualizar a solução desta questão.
Questão:
O valor de Z:
 (Não consigui usar o LATEX para a divisão)
(Não consigui usar o LATEX para a divisão)Bom, eu, inicialmente, resolvi a divisão do
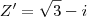 por
por  , mutiplicando pela conjugado do denominador. Deu a seguinte resposta:
, mutiplicando pela conjugado do denominador. Deu a seguinte resposta: ![Z'''= [(\sqrt{3} + 1) + (\sqrt{3} - 1)i / 2]^{(200)} Z'''= [(\sqrt{3} + 1) + (\sqrt{3} - 1)i / 2]^{(200)}](/latexrender/pictures/2c78e0f7df37543e99d2d6670317b89e.png) . Tudo bem até aí. Entretanto, quando fui passar para a potência, pensando em usar Moivre, percebi que o ângulo não era notável e, para piorar, o expoente era muito alto. Eu pensei em decompor o expoente, mas, mesmo assim, eu não sei como encontrar o valor do argumento através do Seno e do Cosseno. Alguém me dá uma orientação na questão?
. Tudo bem até aí. Entretanto, quando fui passar para a potência, pensando em usar Moivre, percebi que o ângulo não era notável e, para piorar, o expoente era muito alto. Eu pensei em decompor o expoente, mas, mesmo assim, eu não sei como encontrar o valor do argumento através do Seno e do Cosseno. Alguém me dá uma orientação na questão?

 sendo que no caso
sendo que no caso  é o angulo da forma trigonométrica e r é o modulo.
é o angulo da forma trigonométrica e r é o modulo.

