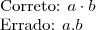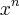 -
- 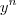 para n inteiro positivo. Bom, eu ''peguei'a prova'' em um livro, mas eu não compreendi alguns artifícios algébricos utilizados pelo autor do livro, por isto estou aqui, para que alguem me ajude a entender. Primeiro vou colocar toda a resolução e depois vou dizer o que não entendi.
para n inteiro positivo. Bom, eu ''peguei'a prova'' em um livro, mas eu não compreendi alguns artifícios algébricos utilizados pelo autor do livro, por isto estou aqui, para que alguem me ajude a entender. Primeiro vou colocar toda a resolução e depois vou dizer o que não entendi.Vamos provar que Provar que
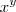 -
- 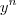 = (x - y) (
= (x - y) ( 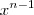 +
+ 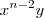 +....+
+....+ 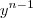 .
.Inicialmente, vamos mostrar que se a
 1,
1, 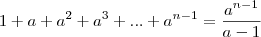
De fato,
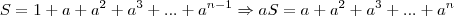
Subtraindo as duas equações anteriores,
aS - S =

 (a-1) S =
(a-1) S = 
 S=
S= 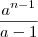
Agora fazendo
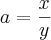 na expressão
na expressão 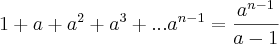 ,
,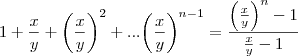

![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow](/latexrender/pictures/b55b363a766543b698e7d099cd436722.png)
![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png)
![{y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow {y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow](/latexrender/pictures/15b4e50dae98cc8b1ce9efe118618abf.png)
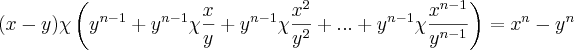
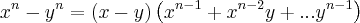
Observação: o símbolo mais apropriado que encontrei para multiplicação foi
 , e só utilizei no final da resolução.
, e só utilizei no final da resolução.Bom, primeiro: aS - S =
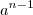
 (a-1) S =
(a-1) S = 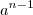
 S=
S= 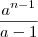
eu realmente não entendi por que aS-S =
 . Entendi que o cara multiplicou ambos os membros da igualdade por a, e na subtração a se corta com a, a² se corta com a² mas não entendi por que
. Entendi que o cara multiplicou ambos os membros da igualdade por a, e na subtração a se corta com a, a² se corta com a² mas não entendi por que 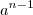 fica fora do resultado da subtração. Ele subtraiu
fica fora do resultado da subtração. Ele subtraiu 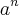 -
- 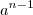 que deu
que deu 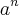 ? Não entendi!
? Não entendi! Bom,nesta parte da equação
![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png) esta expressão
esta expressão 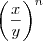 simplesmente some dos colchetes. Por quê?
simplesmente some dos colchetes. Por quê?na penúltima linha, com a equação,
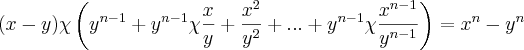 eu já não entendi absolutamente nada. Eu entendi que o cara multiplicou a ambos os membros por
eu já não entendi absolutamente nada. Eu entendi que o cara multiplicou a ambos os membros por 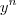 mas não sei como terminou assim.
mas não sei como terminou assim. Bom, é isso. Agradeço muito a quem puder me ajudar a entender. Grato desde já.


 , ou seja, o último termo é
, ou seja, o último termo é  . Multiplicando tudo por
. Multiplicando tudo por  segue
segue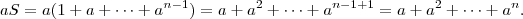
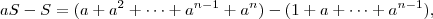
 .
. em evidência e isolando encontramos
em evidência e isolando encontramos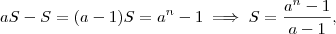
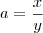 e substituindo,
e substituindo,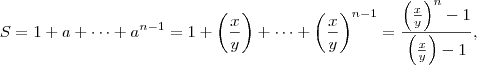
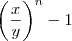 torna-se
torna-se 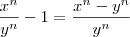 , enquanto que o denominador vira
, enquanto que o denominador vira 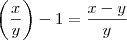 . Multiplicando os dois lados pelo denominador, chegamos na próxima passagem:
. Multiplicando os dois lados pelo denominador, chegamos na próxima passagem:![\left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right). \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right).](/latexrender/pictures/5de74858546adabaaac2da6fdfd9c19a.png)
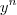 , só que já temos um elemento
, só que já temos um elemento  dividindo, logo subtraimos os expoentes:
dividindo, logo subtraimos os expoentes:![y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/74d6660c3b683ba23dd1f4848f964ff5.png)
![= \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/79b92802e55124b3ff97c9afe9a576fa.png)
![= (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/2032bccab2c290b0a5aa0b4a2fbaaf1b.png)
![= (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n, = (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n,](/latexrender/pictures/e640ec301824444445ba24ddefc0a7a5.png)