 por Jhenrique » Seg Jul 16, 2012 22:44
por Jhenrique » Seg Jul 16, 2012 22:44
Eae galera, blz!?
Bem, eu ñ gosto de depender das definições toscas do ministro da "educação" sobre oq eu devo saber ou ñ...
Então, sou curioso e aprendi a resolver equações cúbicas do tipo x³+px+q=0 com a seguinte fórmula:
x=³?(-q/2+?(q²/4+p³/27))+³?(-q/2-?(q²/4+p³/27))
e com o auxílio desta propriedade:
?(a±?b)=?((a+?(a²-b))/2)±?((a-?(a²-b))/2)
Mas como esse tipo de equação não é prioridade nas escolas e universidades, é dificil achar um material didático decente com mais aprofundamentos...
Sei que é possível reduzir uma equação do tipo ax³+bx²+cx+d=0 para x³+px+q=0.
Algum de vocês sabe como?
Obg,
José H
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Seg Jul 16, 2012 22:53
por Russman » Seg Jul 16, 2012 22:53
Para isto você precisa supor , primeiramente,
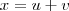
,
por exemplo, onde

e

são valores reais tanto quanto

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Seg Jul 16, 2012 23:36
por Jhenrique » Seg Jul 16, 2012 23:36
nem me lembro mais o que significa u e v, acho que são as raízes polinomiais de 2º ° dum pilinômio de 3º °...
aaah, a dedução não anotei, não lembro e não usei :/
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Ter Jul 17, 2012 00:00
por Russman » Ter Jul 17, 2012 00:00
Se você supor
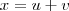
então
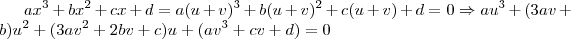
.
Como você deseja reduzir o problema para uma equação de terceiro grau na forma
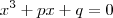
,
temos de provocar que o coeficiente de

se anule. Isto é equivalente a tomar

, pois
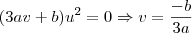
.
Fazendo essa substituição, você obtera uma equação do tipo

, onde
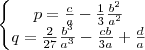
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Ter Jul 17, 2012 13:11
por Jhenrique » Ter Jul 17, 2012 13:11
peraí, vamos por partes... acho q eu notei uma coisa imporante
quando a expressão a(u+v)³+b(u+v)²+c(u+v)+d estava destrinchada na forma de
au³ + 3au²v +3auv² + av³ + bu² + 2buv + bv² + cu + cv + d
vc reagrupou ela num formato polinomial do tipo: "u³...u²...u¹...u?..." e isso rearranjou e mudou a cara e todo o rumo da conta... não imaginei q eu poderia fazer assim!
só tem um detalhe: quando vc rearranjou ela no seu post anterior, esqueceu do bv²...
então tá... quer dizer que sempre que eu tiver uma equação do tipo:
ax³+bx²+cx+d=0
e eu quiser transoformá-la no tipo:
u³+pu+q=0
eu tenho que considerar os seguintes parâmetros:
u = ³?(-q/2+?(q²/4+p³/27))+³?(-q/2-?(q²/4+p³/27))
q = (2/27)*(a³/b³)-(cb/3a)(d/a)
p = (c/a)-(1/3)*(b²/a²)
x = u+v
v = -b/3a
é isso mesmo?? é esta a maneira mais simplificada???
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Ter Jul 17, 2012 18:55
por Russman » Ter Jul 17, 2012 18:55
Em Matemática quando enfrentamos um problema novo é comum tentarmos simplifica-lo, ou transcreve-lo, de forma equivalente a um problema o qual já conheçamos a solução. Note que a mudança de variável
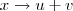
nos permitiu transformar a equação de terceiro grau completa, a qual não conhecemos uma
solução analítica explicita, como na equação de segundo grau, em uma incompleta a qual podemos solucionar
analiticamente.
A solução que eu lhe apresentei é UMA solução possível! Este método é muito eficiente e é conhecido como Método de Cardano-Tartaglia.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Ter Jul 17, 2012 20:29
por Jhenrique » Ter Jul 17, 2012 20:29
Aham, sei, se bem me lembro... naquela época os números negativos eram um orror, e os imaginarios então, nem se fala!
Foi Cardano quem desenvolveu, mas Bombeli, seu aprendiz, foi quem deu a cara à tapa e públicou a fórmula junto com a solução dela envolvendo os complexos...
Eu perguntei se a "fórmula" q vc me passou era a mais simplificada porque sempre que eu tento ler uma literatura a respeito das cúbicas sinto mta dificuldade em fazer a síntese... pq é muita análise... e a explicação de cada literatura está aparentemente diferente da outra :S
por exemplo... essa correspondência entre o P e o Q com os coeficientes ABCD eu ñ havia visto antes... o.0
aff, não tô conseguindo extrair as raízes... de u em função de p e q. Onde vc estudou a fórmula do cardano??
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Arkanus Darondra » Ter Jul 17, 2012 21:50
por Arkanus Darondra » Ter Jul 17, 2012 21:50
Desculpe me intrometer, vim apenas recomendar um link sobre o assunto:
Fórmula de Cardano e TartagliaEspero que seja útil.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Ter Jul 17, 2012 22:04
por Russman » Ter Jul 17, 2012 22:04
Na verdade, não! O método de solução, isto é, a mudança de variável, foi ideia de Tartaglia. Se deve a ele a criação do método. Porém, Tartaglia foi traído por Cardano, a quem havia revelado as fórmulas na promessa de não serem divulgadas. A este fato que se deve o nome Método Cardano-Tartáglia.
É verdade que a evidência dos Números Complexos surgiu nesta época. É um dos grandes feitos da Matemática européia. Bombelli, qe você citou, um excelente matemático italiano, foi quem publicou trabalhos sugerindo que a "raiz quadrada de negativos" era m artifício algébrico através do qual se obtinham as raízes de algumas equações cúbicas chmadas Irredutíveis.Os numeros negativos já eram bem conhecidos na época. Mas tarde, Descartes elevou o status desse artifício a um novo conjunto numérico que chamou de Números Imaginários. Eis então que os Complexos são descobertos.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Ter Jul 17, 2012 22:42
por MarceloFantini » Ter Jul 17, 2012 22:42
Mesmo assim, os números complexos não eram bem aceitos pela comunidade matemática, que não via grande utilidade. Por um pedaço histórico interessante sobre este assunto, veja "Visual Complex Analysis, Tristan Needham". O primeiro capítulo é dedicado à explicar um pouco da história dos números complexos e esclarecer isto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Jul 18, 2012 19:07
por Jhenrique » Qua Jul 18, 2012 19:07
aaah, vlw pela ajuda, mas não tô muito motivado a estudar o link q vc passou como os outros da 1ª pág do google ñ, vejam o pq:
http://pt.wikipedia.org/wiki/Equa%C3%A7 ... %C3%BAbicahttp://www.profcardy.com/cardicas/cardano.phphttp://problemasteoremas.wordpress.com/ ... ou-cubica/cada um explica de uma menira diferente, em algumas explicações faltando incógnitas, outras transbordando de incógnitas... eu hein!!
existe alguma publicação oficial e segura da equação cúbica, onde todos podem se basear para elaborar livros didáticos e fazer consultas, como se fosse a Constituição?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Qua Jul 18, 2012 19:37
por Russman » Qua Jul 18, 2012 19:37
Jhenrique.
Eu acredito que a beleza da Matemática consiste, dentre muitos outros aspectos, na característica de multipla escolha. Ou seja, partindo de pontos diferentes para a solução de um problema você o soluciona da mesma forma, pois chega no mesmo ponto final. Ainda bem que ela funciona assim! Se não, seria muito frustrante a busca de resoluções pois teríamos de encontrar uma única forma dentre inúmeras diferentes que podemos pensar.
A riqueza de métodos para solucionar os mesmos problemas é o que dá personalidade a Matemática. Pense nisso.
Escolha o método que julgue mais adequado e use-o. Se não gostar de nenhum então trabalhe duro e crie o seu próprio! (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Qui Jul 19, 2012 13:02
por Jhenrique » Qui Jul 19, 2012 13:02
Isso é verdade. Na matemática, os fins justificam os meios hehe AHEIhaIO
Mas a fórmula de cardano é a fórmula de cardano, não tem outra. Eu queria ter acesso à publicação feita pelo bombelli, mas o melhor livro didático na minha cidade é do telecurso 2000 (ohmygod!)
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Escrever o vetor em outro formato
por iarapassos » Qui Mar 21, 2013 00:01
- 1 Respostas
- 7418 Exibições
- Última mensagem por young_jedi

Qui Mar 21, 2013 12:38
Álgebra Linear
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7158 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Me Ajudem com este exercicío
por STYLLLER » Ter Set 07, 2010 17:35
- 2 Respostas
- 1642 Exibições
- Última mensagem por STYLLLER

Qua Set 08, 2010 12:50
Polinômios
-
- nao sei com terminar este calculo
por weverton » Sex Out 08, 2010 18:05
- 1 Respostas
- 3147 Exibições
- Última mensagem por Elcioschin

Sex Out 08, 2010 18:13
Geometria Analítica
-
- eliminar este tópico
por anaqs » Qui Jun 25, 2015 14:12
- 0 Respostas
- 2933 Exibições
- Última mensagem por anaqs

Sáb Jul 25, 2015 19:23
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



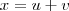 ,
, e
e  são valores reais tanto quanto
são valores reais tanto quanto  .
.

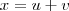
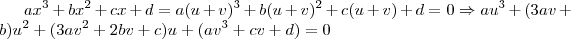 .
.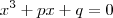 ,
, se anule. Isto é equivalente a tomar
se anule. Isto é equivalente a tomar  , pois
, pois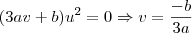 .
. , onde
, onde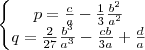 .
.

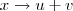 nos permitiu transformar a equação de terceiro grau completa, a qual não conhecemos uma solução analítica explicita, como na equação de segundo grau, em uma incompleta a qual podemos solucionar analiticamente.
nos permitiu transformar a equação de terceiro grau completa, a qual não conhecemos uma solução analítica explicita, como na equação de segundo grau, em uma incompleta a qual podemos solucionar analiticamente.








