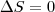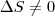Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Qua Jul 18, 2012 10:24
por Cleyson007 » Qua Jul 18, 2012 10:24
Bom dia a todos!
Conside o treinamento de um atleta para um corrida em um pista de 1500m de comprimento. Suponha que ele vá de um extremo ao outro inúmeras vezes mudando o sentido de seu movimento somente quando atinge um dos extremos. Suponha também que em t = t0 ele inicie seu movimento de O (origem da pista de atletismo), que em t = t1 ele atinja pela primeira vez o ponto F (final da pista), que em t = t2 ele atinja o ponto O novamente e assim sucessivamente, de modo que em t = t2n-1, n = 1,2,..., ele se encontre em F, pela n-ésima vez, e em t = t2n-2, ele se encontre em O, pela n-ésima vez.
a) Calcule o deslocamento do atleta nos intervalos: [t0,t1], [t1,t2], [t0,t2], [t0,t7] e [t1,t8].
Vou postar minha resolução abaixo para verem se está correto.
Até logo.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qua Jul 18, 2012 11:54
por Cleyson007 » Qua Jul 18, 2012 11:54
Amigos, resolvi da seguinte forma:
a) Deslocamento no intervalo [t0,t1]:
O atleta inicia em O (origem da pista) no tempo t0 e chega em F (final da pista) no instante t1. Logo, 1500m.
Deslocamento no intervalo [t1,t2]:
O atleta parte de F (final da pista) e volta para O (origem da pista). Logo, -1500m.?
Deslocamento no intervalo [t0,t2]:
O atleta percorre os 1500m do instante [t0,t1] mais os 1500m do instante [t1,t2]. Logo, 3000m.
Deslocamento nos intervalos [t0,t7] e [t1,t8]:
--> Qual a maneira mais fácil de encontrar os deslocamentos em questão?
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Arkanus Darondra » Qua Jul 18, 2012 13:08
por Arkanus Darondra » Qua Jul 18, 2012 13:08
Cleyson007 escreveu:Deslocamento no intervalo [t0,t1]:
O atleta inicia em O (origem da pista) no tempo t0 e chega em F (final da pista) no instante t1. Logo, 1500m.
Certo.
Cleyson007 escreveu:Deslocamento no intervalo [t1,t2]:
O atleta parte de F (final da pista) e volta para O (origem da pista). Logo, -1500m.?
Certo. Uma vez que o deslocamento depende da orientação da trajetória e o atleta está indo contra ela, seu deslocamento será negativo.
Cleyson007 escreveu:Deslocamento no intervalo [t0,t2]:
O atleta percorre os 1500m do instante [t0,t1] mais os 1500m do instante [t1,t2]. Logo, 3000m.
Errado. Isso seria a distância percorrida.
Cleyson007 escreveu:--> Qual a maneira mais fácil de encontrar os deslocamentos em questão?
Sendo

: Você deve ter notado que quando x é par s = 0 e quando x é ímpar s = 1500m.
Como o deslocamento depende apenas dos espaços inicial e final, basta que você faça:

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qua Jul 18, 2012 17:09
por Cleyson007 » Qua Jul 18, 2012 17:09
Boa tarde Arkanus Darondra!
Obrigado por ajudar! Refiz. Por favor veja se está correto, ok?
Deslocamento no intervalo [t0,t2]:
Será 0m? Estou pensando que o atleta correu os 1500m instante [t0,t1] e retornou ao ponto de origem O.
Deslocamento nos intervalos [t0,t7]:
1500m --> (Final: 1500m - Inicial 0m)
Deslocamento no intervalo [t1,t8]:
0m (em t8) - 1500m (em t1) = -1500m
Por favor me ajude com esse:
b) Calcule o deslocamento do atleta no intervalo [tn,tn+n']; discuta separadamente os casos em que n' é par e n' é ímpar.
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qui Jul 19, 2012 09:33
por Cleyson007 » Qui Jul 19, 2012 09:33
Outra dúvida:
Qual a quantidade de vezes em que o atlta deverá percorrer a pista (mover de um extremo ao outro) para que tenha percorrido a distância de 42Km?
Posso resolver assim? --> 1,5km (x) = 42Km <--> x = 28 vezes
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Arkanus Darondra » Qui Jul 19, 2012 14:27
por Arkanus Darondra » Qui Jul 19, 2012 14:27
Os itens a e "c" estão corretos.
Quanto ao item b, ainda não tenho a resposta porque o item não diz que posso analisar se n é par ou ímpar (apenas n'). Assim que tiver, eu posto aqui caso ninguém tenha respondido.
Até agora, fiz assim:
n' par)n par ou ímpar: 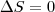 n' ímpar)n par:
n' ímpar)n par:  n ímpar:
n ímpar: 
Ou:
n' par)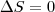 n' ímpar)
n' ímpar)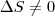
Não acho que esteja correto, pois no primeiro caso eu também analisei os casos em que n é par e/ou ímpar; e no segundo, não calculei o deslocamento para n' ímpar.
Se alguém souber como fazer, poste aqui.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 : Você deve ter notado que quando x é par s = 0 e quando x é ímpar s = 1500m.
: Você deve ter notado que quando x é par s = 0 e quando x é ímpar s = 1500m.