 por Rafael16 » Seg Jul 16, 2012 21:49
por Rafael16 » Seg Jul 16, 2012 21:49
Olá pessoal,
Determine três números em P.G., de tal forma que a soma do segundo com o terceiro seja 60 e a diferença entre o segundo e o primeiro seja 10.Resolução:Dados do exercício:
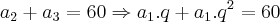
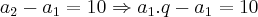
Colocando essas equações acima em um sistema, achei:
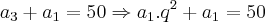
Tentei fazer isso de tudo quanto é jeito, jogando na fórmula do soma
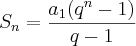
e também na propriedade
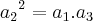 Resposta: (5,15,45)ou(10,20,40)
Resposta: (5,15,45)ou(10,20,40)P.G. é bem mais difícil que P.A.

Valeu gente!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Arkanus Darondra » Seg Jul 16, 2012 21:58
por Arkanus Darondra » Seg Jul 16, 2012 21:58
Você montou o sistema corretamente, basta continuar colocando a1 em evidência.
Resultará numa equação polinomial do segundo grau com as raízes 2 e 3 (razão).
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Seg Jul 16, 2012 22:05
por Russman » Seg Jul 16, 2012 22:05
Realmente, seu sistema esta montado de forma correta! Este não é linear. Então eu, pessoalmente, sugiro que você
isole o valor 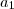 em ambas equações
em ambas equações e os iguale pois , de fato, sao iguais. Com isso, você obterá uma equação onde a incógnita é somente o valor da razão da P.G..
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rafael16 » Seg Jul 16, 2012 22:11
por Rafael16 » Seg Jul 16, 2012 22:11
Arkanus Darondra escreveu:Você montou o sistema corretamente, basta continuar colocando a1 em evidência.
Resultará numa equação polinomial do segundo grau com as raízes 2 e 3 (razão).
Valeu Arkanus Darondra,
Só que eu cheguei nessa equação
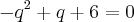
dando como resposta
x' = -2 e x''=3
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Seg Jul 16, 2012 22:17
por Russman » Seg Jul 16, 2012 22:17
A equação que você deve obter é
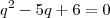
,
cujas soluções são as que o amigo acima te disse.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Arkanus Darondra » Seg Jul 16, 2012 22:19
por Arkanus Darondra » Seg Jul 16, 2012 22:19
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4252 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4724 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25545 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4234 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2888 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
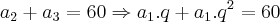
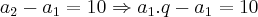
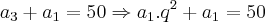
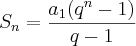
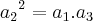


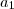 em ambas equações
em ambas equações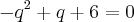
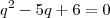 ,
,
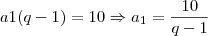
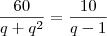
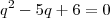

 .
.



