 com os eixos coordenados.
com os eixos coordenados.Se alguém puder dar dicas de como iniciar exercício, ficarei grato.

 com os eixos coordenados.
com os eixos coordenados.

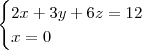
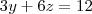 e
e 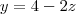 , que é uma reta. Os outros casos são semelhantes.
, que é uma reta. Os outros casos são semelhantes.

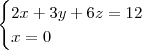
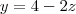
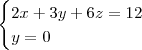
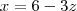
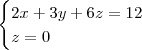
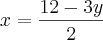
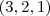



Claudin escreveu:Determine as interseções do planocom os eixos coordenados.
Se alguém puder dar dicas de como iniciar exercício, ficarei grato.
Russman escreveu:As equações dos eixos coordenados são, respectivamente, x=0, y=0 e z=0. As interssecções serão retas.
MarceloFantini escreveu:De uma certa forma, sim. Resolvendo o sistema
vem quee
, que é uma reta. Os outros casos são semelhantes.
 com o eixo x irá ocorrer quando x = t, y = 0 e z = 0. Substituindo esses valores na equação do plano obtemos t = 6. Portanto, o ponto de interseção do plano com o eixo x é (6, 0, 0).
com o eixo x irá ocorrer quando x = t, y = 0 e z = 0. Substituindo esses valores na equação do plano obtemos t = 6. Portanto, o ponto de interseção do plano com o eixo x é (6, 0, 0).

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)