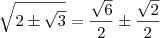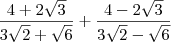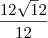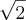por Tibinhas » Seg Jun 25, 2012 19:24
por Tibinhas » Seg Jun 25, 2012 19:24
![\frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}} \frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}}](/latexrender/pictures/187def60b0b7259032627642ead1730a.png)
O exercício pede para simplificar essa expressão, na resposta esta
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
tentei raciona-la fazendo a diferença de dois quadrados, mas cai em uma conta muito dificil
-
Tibinhas
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 25, 2012 18:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por emsbp » Sáb Jul 07, 2012 18:13
por emsbp » Sáb Jul 07, 2012 18:13
Boa tarde.
Também tentei racionalizar e não cheguei à solução indicada.
Explico o meu raciocínio:
1º racionalizei as duas parcelas, utilizando o conjugado do denominador.
2º simplifiquei ao máximo o numerador, ficando com denominador igual a 3.
Seguiu o mesmo processo?
Obrigado
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por Arkanus Darondra » Sáb Jul 07, 2012 22:29
por Arkanus Darondra » Sáb Jul 07, 2012 22:29
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Sáb Jul 07, 2012 22:29
por Arkanus Darondra » Sáb Jul 07, 2012 22:29
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- racionalização de denominadores
por Claudia Silva » Qua Jun 22, 2011 21:15
- 1 Respostas
- 1755 Exibições
- Última mensagem por FilipeCaceres

Qua Jun 22, 2011 22:10
Álgebra Elementar
-
- Racionalização de denominadores
por LuizCarlos » Qua Mai 09, 2012 15:10
- 2 Respostas
- 1826 Exibições
- Última mensagem por LuizCarlos

Qua Mai 09, 2012 18:54
Álgebra Elementar
-
- racionalização de denominadores
por cafinfa » Dom Mai 20, 2012 16:43
- 3 Respostas
- 2947 Exibições
- Última mensagem por Molina

Dom Mai 20, 2012 17:19
Sistemas de Equações
-
- racionalização de denominadores
por cafinfa » Dom Mai 20, 2012 17:16
- 1 Respostas
- 1418 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:21
Álgebra Elementar
-
- Racionalização de denominadores
por Thais Aquino Lima » Ter Fev 12, 2013 08:07
- 1 Respostas
- 1216 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 11:17
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}} \frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}}](/latexrender/pictures/187def60b0b7259032627642ead1730a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)

![\frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}} \frac{2+\sqrt[]{3}}{\sqrt[]{2}+\sqrt[]{2+\sqrt[]{3}}}+\frac{2-\sqrt[]{3}}{\sqrt[]{2}-\sqrt[]{2-\sqrt[]{3}}}](/latexrender/pictures/187def60b0b7259032627642ead1730a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)


![\displaystyle\frac{[(2+\sqrt3)(\sqrt2-\sqrt{2-\sqrt3})]+[(2-\sqrt3)(\sqrt2+\sqrt{2+\sqrt3})]}{(\sqrt2+\sqrt{2+\sqrt3})(\sqrt2-\sqrt{2-\sqrt3})} \displaystyle\frac{[(2+\sqrt3)(\sqrt2-\sqrt{2-\sqrt3})]+[(2-\sqrt3)(\sqrt2+\sqrt{2+\sqrt3})]}{(\sqrt2+\sqrt{2+\sqrt3})(\sqrt2-\sqrt{2-\sqrt3})}](/latexrender/pictures/a59c36307c1b432197f1c1f7efca3de0.png)

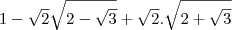

![\left[{1-\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right] \left[{1-\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]](/latexrender/pictures/73500608ed6818c25b5897080160b25e.png)
![\left[{1+\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]= \left[{1+\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]=](/latexrender/pictures/6942ab25ae4806e0f3bfcb2f0a1525f5.png)
![= 1^2-\left[\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]^2 = 1^2-\left[\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]^2](/latexrender/pictures/9cbd1086bbc46f7167f8b562eb21f5bd.png)

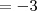
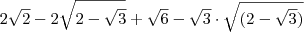
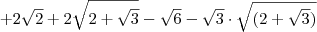


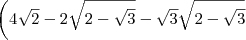

![\left[{1+\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right] \left[{1+\sqrt{2}\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\right]](/latexrender/pictures/94a4d84b15d30876fb711a96e802684a.png)
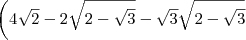
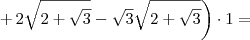
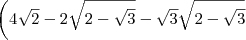

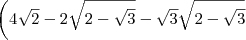

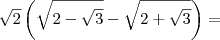

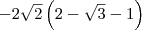
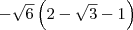


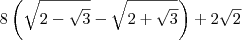
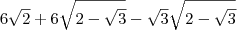
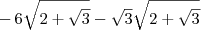

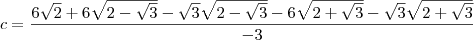



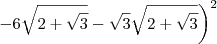

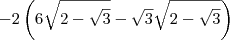
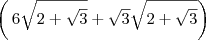




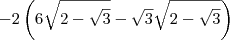

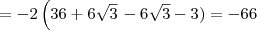



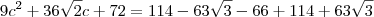
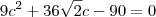

 e
e  .
.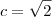 .
.