Estou encontrando muita dificuldade para montar as equações do problema abaixo. Alguém pode me ajudar?
--> Hoje a soma das idades do Adriano, Bruno, Carlos e do Daniel é igual a 159 anos.
Quando o Carlos tinha o dobro da idade do Daniel,o Bruno tinha 28 anos.
Quando o Bruno tinha o triplo da idade do Daniel,o Adriano tinha 37 anos.
Quando o Adriano tinha o quádruplo da idade do Daniel,o produto das idades deles quatro era igual a 159.732. Qual a idade de cada um hoje?
Estou tentando assim: *Chamando de A a idade atual do Adriano.
*Chamando de B a idade atual do Bruno.
*Chamando de C a idade atual do Carlos.
*Chamando de D a idade atual do Daniel.
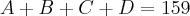
Como montar as outras equações?
Agradeço sua ajuda.
Até mais.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)