 por Crouff » Qui Jul 05, 2012 11:55
por Crouff » Qui Jul 05, 2012 11:55
Ajuda com o exercício abaixo:
Resolver a Equação (U=R)

Comecei com esse desenvolvimento:
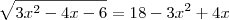
 ________________________
________________________ com
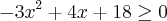
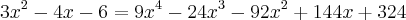
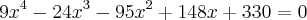
Mais ai resulta em polinômio de grau 4... Acredito que estou pegando o caminho errado para resolver.
Agradeço desde ja.
Editado pela última vez por
Crouff em Qui Jul 05, 2012 12:19, em um total de 1 vez.
-
Crouff
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 05, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica, gestão
- Andamento: cursando
 por e8group » Qui Jul 05, 2012 12:19
por e8group » Qui Jul 05, 2012 12:19
Sugestão ! Se você atribuir uma variável a

,por exemplo

= p basta achar p e depois achar o valor para x ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Crouff » Qui Jul 05, 2012 12:29
por Crouff » Qui Jul 05, 2012 12:29
Boa sugestão,
Conseguir desenvolver, e o resultado bateu com o gabarito
Muito Obrigado

-
Crouff
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 05, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica, gestão
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função F] Não consigo desenvolver esse exercício
por thayna_rosa » Seg Nov 12, 2012 18:35
- 4 Respostas
- 2322 Exibições
- Última mensagem por thayna_rosa

Seg Nov 12, 2012 20:58
Funções
-
- Fatoração - esse consegui desenvolver
por IsadoraLG » Qua Jul 09, 2014 21:47
- 1 Respostas
- 1079 Exibições
- Última mensagem por DanielFerreira

Qua Jul 16, 2014 20:41
Álgebra Elementar
-
- não lembro mito bem como se resolve esse exercicio de log
por joaoalbertotb » Sex Set 18, 2009 12:56
- 1 Respostas
- 2005 Exibições
- Última mensagem por Elcioschin

Sex Set 18, 2009 22:17
Logaritmos
-
- Como resolvo esse problema envolvendo equação?
por LuizCarlos » Ter Jul 26, 2011 17:15
- 2 Respostas
- 4548 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 18:30
Sistemas de Equações
-
- como resolvo esse problema de sistema de equação?
por kellen e winicius » Ter Ago 30, 2011 00:13
- 3 Respostas
- 5073 Exibições
- Última mensagem por Caradoc

Ter Ago 30, 2011 20:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

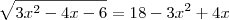
 ________________________ com
________________________ com 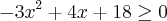
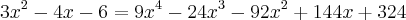
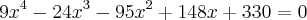


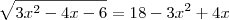
 ________________________ com
________________________ com 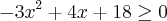
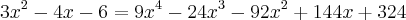
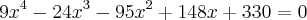

 ,por exemplo
,por exemplo  = p basta achar p e depois achar o valor para x ...
= p basta achar p e depois achar o valor para x ...



 .
.



