 por DanielFerreira » Dom Jul 01, 2012 12:07
por DanielFerreira » Dom Jul 01, 2012 12:07
danjr5 escreveu:Use o Teorema de Stokes para calcular
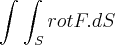
, onde
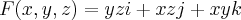
e S é a parte da esfera
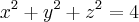
que está dentro do cilindro

e acima do plano

Tentei assim:
Calculei o rotacional e encontrei zero;
De acordo com a definição

C => intersecção entre as superfícies;

, já que,
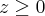
Parametrizando o cilindro:
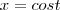


Então,
![\sigma(t) = (cost, sent, \sqrt[]{3}), 0 \leq t \leq 2\pi \sigma(t) = (cost, sent, \sqrt[]{3}), 0 \leq t \leq 2\pi](/latexrender/pictures/726aa8be6bfbf3c5650407943495e799.png)
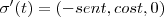
e,
![F(\sigma(t)) = (\sqrt[]{3}sent, \sqrt[]{3}cost, sent.cost) F(\sigma(t)) = (\sqrt[]{3}sent, \sqrt[]{3}cost, sent.cost)](/latexrender/pictures/ee91825fee4c9c6f21461fa0db96e528.png)
Daí,
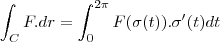
![\int_{C}^{}F.dr = \int_{0}^{2\pi}(- \sqrt[]{3}.sen^2t + \sqrt[]{3}.cos^2t + 0) dt \int_{C}^{}F.dr = \int_{0}^{2\pi}(- \sqrt[]{3}.sen^2t + \sqrt[]{3}.cos^2t + 0) dt](/latexrender/pictures/d4ddb142b627a2918c6ee42a6446bbbe.png)
![\int_{C}^{}F.dr = \int_{0}^{2\pi}\sqrt[]{3}.cos^2tdt \int_{C}^{}F.dr = \int_{0}^{2\pi}\sqrt[]{3}.cos^2tdt](/latexrender/pictures/38c07145f16092930603c51b7e60e71d.png)
...
![\int_{C}^{}F.dr = \pi\sqrt[]{3} \int_{C}^{}F.dr = \pi\sqrt[]{3}](/latexrender/pictures/32f76a47fb6ca93d56c027a09d4f4097.png)
Segundo o gabarito do livro, a resposta correta é
zero.
Onde estou errando?
Desde já agradeço.
Att,
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Renato_RJ » Seg Jul 02, 2012 11:42
por Renato_RJ » Seg Jul 02, 2012 11:42
Campeão, se o rotacional é zero, então o resultado será zero, veja:
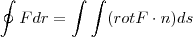
Acredito eu...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Russman » Seg Jul 02, 2012 18:58
por Russman » Seg Jul 02, 2012 18:58
Realmente, veja que


.
Portanto,
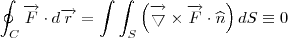
.
Mas, fazendo pela integral de linha, você desenvolveu certo, porém, na ultima passagem, o correto é integrar
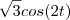
de


que é zero!
Entende?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sex Jul 06, 2012 20:04
por DanielFerreira » Sex Jul 06, 2012 20:04
Russman,
corrija-me se estiver errado, por favor!

pois está acima do plano

?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sáb Jul 07, 2012 02:52
por MarceloFantini » Sáb Jul 07, 2012 02:52
Não, o parâmetro deve variar entre 0 e

, senão você pega apenas metade do cilindro. Aí sim
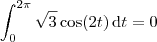
. Estar acima do plano

quer dizer
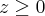
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sáb Jul 07, 2012 11:50
por DanielFerreira » Sáb Jul 07, 2012 11:50
Vlw MarceloFantini.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Russman » Sáb Jul 07, 2012 19:52
por Russman » Sáb Jul 07, 2012 19:52
Isto...na hora de digitar saiu errado..é de 0 a 2pi. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por DanielFerreira » Sáb Jul 07, 2012 20:29
por DanielFerreira » Sáb Jul 07, 2012 20:29

Russman,
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo III] - Teorema de Stokes
por Feliperpr » Sáb Abr 21, 2012 16:08
- 5 Respostas
- 2627 Exibições
- Última mensagem por Feliperpr

Sáb Abr 21, 2012 19:33
Cálculo: Limites, Derivadas e Integrais
-
- Stokes e divergencia
por Felipe Silva » Ter Jun 08, 2010 18:54
- 0 Respostas
- 971 Exibições
- Última mensagem por Felipe Silva

Ter Jun 08, 2010 18:54
Cálculo: Limites, Derivadas e Integrais
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3260 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4669 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3510 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
, onde
e S é a parte da esfera
que está dentro do cilindro
e acima do plano

 , já que,
, já que,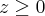
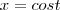


![\sigma(t) = (cost, sent, \sqrt[]{3}), 0 \leq t \leq 2\pi \sigma(t) = (cost, sent, \sqrt[]{3}), 0 \leq t \leq 2\pi](/latexrender/pictures/726aa8be6bfbf3c5650407943495e799.png)
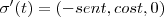
![F(\sigma(t)) = (\sqrt[]{3}sent, \sqrt[]{3}cost, sent.cost) F(\sigma(t)) = (\sqrt[]{3}sent, \sqrt[]{3}cost, sent.cost)](/latexrender/pictures/ee91825fee4c9c6f21461fa0db96e528.png)
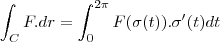
![\int_{C}^{}F.dr = \int_{0}^{2\pi}(- \sqrt[]{3}.sen^2t + \sqrt[]{3}.cos^2t + 0) dt \int_{C}^{}F.dr = \int_{0}^{2\pi}(- \sqrt[]{3}.sen^2t + \sqrt[]{3}.cos^2t + 0) dt](/latexrender/pictures/d4ddb142b627a2918c6ee42a6446bbbe.png)
![\int_{C}^{}F.dr = \int_{0}^{2\pi}\sqrt[]{3}.cos^2tdt \int_{C}^{}F.dr = \int_{0}^{2\pi}\sqrt[]{3}.cos^2tdt](/latexrender/pictures/38c07145f16092930603c51b7e60e71d.png)
![\int_{C}^{}F.dr = \pi\sqrt[]{3} \int_{C}^{}F.dr = \pi\sqrt[]{3}](/latexrender/pictures/32f76a47fb6ca93d56c027a09d4f4097.png)



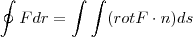


 .
.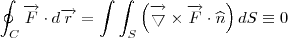 .
.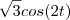 de
de 
 que é zero!
que é zero! pois está acima do plano
pois está acima do plano  , senão você pega apenas metade do cilindro. Aí sim
, senão você pega apenas metade do cilindro. Aí sim 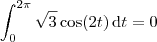 . Estar acima do plano
. Estar acima do plano 

 Russman,
Russman,