
Questões:
49-69. Encontre os valores máximo e mínimo aboslutos de f no intervalo dado.
Por exemplo questão .50 do livro.
f(x) = x³ - 3x + 1, [0 , 3]
f(1) = 1³ - 3.1 + 1
f(1) = -1
Aqui seria "Mínimo absoluto"?
f(3) = 3³ - 3 . 3 + 1
f(3) = 27 - 9 + 1
f(3) = 19
Aqui seria "Máximo absoluto"?
-----------------------------------------------------------------------------
Por exemplo: Usei assim pra achar o "Mínimo absoluto"
Questão 52.
f(x) = 18x + 15x² - 4x³, [-3 , 2]
f(x) = 18 + 30x - 12x²
f(x) = 18 + 30.(-1) - 12.(-1)²
f(x) = 0
Então, Menor abosluto: (x = -1)
E pra achar o máximo absoluto mais rápido?
-----------------------------------------------------------------------------
Dúvidas:
1. Como faço pra achar o ponto critico?
2. Como faço pra achar a "valor médio"?
3. Como faço pra achar diretamente o "maximo" e o "minimo"? Seria uma teoria isso?
-----------------------------------------------------------------------------
Agradeço pela atenção de todos.
Abraço!



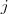 uma função ,dizemos que x é ponto crítico de
uma função ,dizemos que x é ponto crítico de 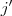 ) é nula ou não existe(
) é nula ou não existe( tal que
tal que 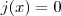 ) .
) .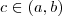 tal que
tal que 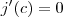 .
.![j(x_0) \geq j(x) \forall x \in [a,b] j(x_0) \geq j(x) \forall x \in [a,b]](/latexrender/pictures/4ccb3e806719c65f52e9f1aa373c84d8.png) e
e![j(x_0) \leq j(x)\forall x\in [a,b] j(x_0) \leq j(x)\forall x\in [a,b]](/latexrender/pictures/f5a17326f6538e48214b9ec1a0012adb.png) ....
....
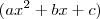 onde
onde  são constantes com
são constantes com  os extremos pode ser obtidos por
os extremos pode ser obtidos por 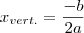 e
e 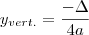 .
. . se
. se  temos um ponto de máximo caso contrário temos um ponto de mínimo .
temos um ponto de máximo caso contrário temos um ponto de mínimo .