 por Luthius » Sex Jul 31, 2009 11:19
por Luthius » Sex Jul 31, 2009 11:19
Bom dia pessoal, gostaria do passo a passo para encontrar o valor de 'a' no limite abaixo.
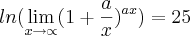
Alguém pode me ajudar?
Abraço
Luthius
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Molina » Sex Jul 31, 2009 14:38
por Molina » Sex Jul 31, 2009 14:38
Luthius escreveu:Bom dia pessoal, gostaria do passo a passo para encontrar o valor de 'a' no limite abaixo.
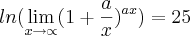
Alguém pode me ajudar?
Abraço
Luthius
Questão realmente intrigante. Como você já tentou resolve-la?
Eu começaria elevando ambos os lados por
e.
Seria uma saída pra eliminar o ln.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Felipe Schucman » Sex Jul 31, 2009 15:06
por Felipe Schucman » Sex Jul 31, 2009 15:06
Luthius escreveu:Bom dia pessoal, gostaria do passo a passo para encontrar o valor de 'a' no limite abaixo.
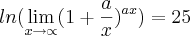
Alguém pode me ajudar?
Abraço
Luthius
Bom dia,
Acho que começaria um pouco diferente do molina, tentaria utilizar um limite famoso que é

, tentaria chegar nisso com alguma mudança de incognita talvez, a partir dai resolveria o resto....não sei se da certo assim depois vou tentar!
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Felipe Schucman » Sex Jul 31, 2009 19:39
por Felipe Schucman » Sex Jul 31, 2009 19:39
Luthius escreveu:Bom dia pessoal, gostaria do passo a passo para encontrar o valor de 'a' no limite abaixo.
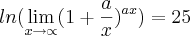
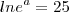
Alguém pode me ajudar?
Abraço
Luthius
Ola! Pensei em algo que bnão tenho certeza que é correto mas talvez seja.... no caso
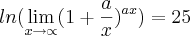
, independente do numero que a for a fração a/x ira tender a aproximadamente o mesmo numero pois x aumente infinitamente fazendo com que a fração tenda a 0...então,
Faria o seguinte,

---->

que é,
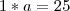
---> usando regras de logaritmos, o a cai, e o lne é a mesma coisa que 1, de que a=25....
Não tenho certeza disso, mas é um resolução que tentei....
Se alguém mais entendido de calculo aparecer porfavor aponte algum erro,
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Molina » Sex Jul 31, 2009 23:34
por Molina » Sex Jul 31, 2009 23:34
Felipe Schucman escreveu:Luthius escreveu:Bom dia pessoal, gostaria do passo a passo para encontrar o valor de 'a' no limite abaixo.
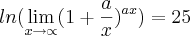
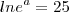
Alguém pode me ajudar?
Abraço
Luthius
Ola! Pensei em algo que bnão tenho certeza que é correto mas talvez seja.... no caso
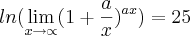
, independente do numero que a for a fração a/x ira tender a aproximadamente o mesmo numero pois x aumente infinitamente fazendo com que a fração tenda a 0...então,
Faria o seguinte,

---->

que é,
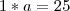
---> usando regras de logaritmos, o a cai, e o lne é a mesma coisa que 1, de que a=25....
Não tenho certeza disso, mas é um resolução que tentei....
Se alguém mais entendido de calculo aparecer porfavor aponte algum erro,
Um abraço!
Boa noite.
Acho que é isso mesmo.
Não notei aquele limite fundamental...
Só montando agora em uma única expressão:
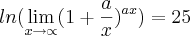


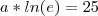
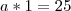

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Jul 31, 2009 23:36
por Molina » Sex Jul 31, 2009 23:36
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Felipe Schucman » Sáb Ago 01, 2009 00:46
por Felipe Schucman » Sáb Ago 01, 2009 00:46
Acho que é um definição correta com tanto que aquilo seja mesmo um limite fundamental, o que temos que descobrir é se é um limite fundamental mesmo, talvez substituindo a por 25 e tentando chegar ao resultado saberemos.... tentar aproximar com uma boa calculadora o x a um valor bem alto....
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Elcioschin » Sáb Ago 01, 2009 11:49
por Elcioschin » Sáb Ago 01, 2009 11:49
Limite (1 + 1/y)^y = e ----> Limite fundamental
y -->oo
Limite (1 + a/x)^ax = 25 ----> Fazendo a/x = 1/y -----> x = ay ----> x-->oo ----> y-->oo
x -->oo
Limite (1 + 1/y)^a*(ay) = 25
y -->oo
Limite (1 + 1/y)^a²y = 25
y -->oo
[Limite (1 + 1/y)^y]^a² = 25
y-->00
e^a² = 25 ----> (e^a)² = 5² ----> e^a = 5 -----> a = ln5
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Felipe Schucman » Sáb Ago 01, 2009 13:40
por Felipe Schucman » Sáb Ago 01, 2009 13:40
Elcioschin escreveu:Limite (1 + 1/y)^y = e ----> Limite fundamental
y -->oo
Limite (1 + a/x)^ax = 25 ----> Fazendo a/x = 1/y -----> x = ay ----> x-->oo ----> y-->oo
x -->oo
Limite (1 + 1/y)^a*(ay) = 25
y -->oo
Limite (1 + 1/y)^a²y = 25
y -->oo
[Limite (1 + 1/y)^y]^a² = 25
y-->00
e^a² = 25 ----> (e^a)² = 5² ----> e^a = 5 -----> a = ln5
Bom Dia Elcioschin,
Realmente acho que essa resolução ta certa, porém a resposta ficaria

----->

-----
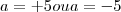
Obrigado Elcioschin
Um Abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Elcioschin » Dom Ago 02, 2009 21:19
por Elcioschin » Dom Ago 02, 2009 21:19
Felipe
Eu cometí um engano na última linha, mas a solução é outra:
e^(a²) = 25 -----> Aplicando logaritmo na base e (ln) nos dois membros:
ln[e^(a²)] = ln25 ----> (a²)lne = ln25 ----> a² = ln25 ----> a = [ln25]^(1/2) ----> a = V[ln25]
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Luthius » Seg Ago 03, 2009 10:04
por Luthius » Seg Ago 03, 2009 10:04
Fiquei em dúvida.
Eu concordo em ser um limite fundamental e a resposta ser 25.
Mas a outra proposição não me deixa certo sobre o resultado.
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Elcioschin » Seg Ago 03, 2009 12:17
por Elcioschin » Seg Ago 03, 2009 12:17
Felipe
Você está coberto de razão: somente agora eu vi que, na expressão original, existe o ln antes do limite.
Você pode ver que, em toda a minha demonstração, eu calculei APENAS o limite. Complementando:
ln[e^(a²)] = 25 -----> a²*lne = 5² ----> a²*1 = 5² ---> a² = 5² ----> a = +5 ou a = -5
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Luthius » Seg Ago 03, 2009 15:26
por Luthius » Seg Ago 03, 2009 15:26
Então a resposta seguindo um passo a passo é:
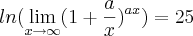
Dado o seguinte limite fundamental de Euler.
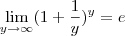
Fazendo

em

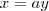
Substituindo na fórmula:

Substituindo novamente:
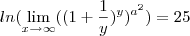

Aplicando uma das leis dos logaritmos:
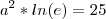
![{a}=\sqrt[]{25} {a}=\sqrt[]{25}](/latexrender/pictures/b25d3a4cbfadd2b4666594f19a707b4f.png)

ou

Obrigado pessoal, pelo grande apoio.
Obs.:Corrigi o erro conforme informado pelo nosso colega.
Editado pela última vez por
Luthius em Ter Ago 04, 2009 08:39, em um total de 2 vezes.
-
Luthius
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 30, 2009 09:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Elcioschin » Seg Ago 03, 2009 19:02
por Elcioschin » Seg Ago 03, 2009 19:02
Luthius
Uma pequena correção ----> Fazendo a/x = 1/y
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite Função Exponencial] Qual o valor?
por Ronaldobb » Qui Nov 01, 2012 10:21
- 1 Respostas
- 1773 Exibições
- Última mensagem por young_jedi

Qui Nov 01, 2012 13:51
Cálculo: Limites, Derivadas e Integrais
-
- Qual o valor de K?
por Talvane Ramos » Ter Mar 23, 2010 13:12
- 2 Respostas
- 4488 Exibições
- Última mensagem por joao_pimentel

Qua Dez 14, 2011 20:21
Sistemas de Equações
-
- Qual o valor de (-1)^2/6?
por Abelardo » Ter Abr 12, 2011 23:55
- 28 Respostas
- 15565 Exibições
- Última mensagem por MarceloFantini

Ter Fev 14, 2012 16:26
Álgebra Elementar
-
- Qual é o valor de m
por andersontricordiano » Ter Mai 10, 2011 21:58
- 2 Respostas
- 1999 Exibições
- Última mensagem por DanielRJ

Ter Mai 10, 2011 22:32
Funções
-
- qual é o valor de x na equação:
por aninha1701 » Qui Mar 12, 2009 11:56
- 2 Respostas
- 7300 Exibições
- Última mensagem por Molina

Qui Mar 12, 2009 17:38
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
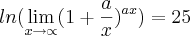

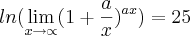



 , tentaria chegar nisso com alguma mudança de incognita talvez, a partir dai resolveria o resto....não sei se da certo assim depois vou tentar!
, tentaria chegar nisso com alguma mudança de incognita talvez, a partir dai resolveria o resto....não sei se da certo assim depois vou tentar!
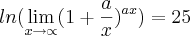
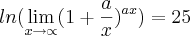 , independente do numero que a for a fração a/x ira tender a aproximadamente o mesmo numero pois x aumente infinitamente fazendo com que a fração tenda a 0...então,
, independente do numero que a for a fração a/x ira tender a aproximadamente o mesmo numero pois x aumente infinitamente fazendo com que a fração tenda a 0...então, ---->
----> 
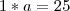 ---> usando regras de logaritmos, o a cai, e o lne é a mesma coisa que 1, de que a=25....
---> usando regras de logaritmos, o a cai, e o lne é a mesma coisa que 1, de que a=25....
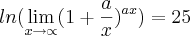
, independente do numero que a for a fração a/x ira tender a aproximadamente o mesmo numero pois x aumente infinitamente fazendo com que a fração tenda a 0...então,
---->
---> usando regras de logaritmos, o a cai, e o lne é a mesma coisa que 1, de que a=25....
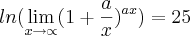


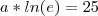
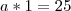








 ----->
----->  -----
----- 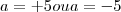




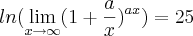
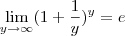
 em
em 
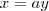

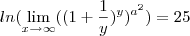

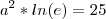
![{a}=\sqrt[]{25} {a}=\sqrt[]{25}](/latexrender/pictures/b25d3a4cbfadd2b4666594f19a707b4f.png)



