 por washington_araujo » Ter Jun 26, 2012 10:28
por washington_araujo » Ter Jun 26, 2012 10:28
Não existem soluções racionais para a equação x^5 + x^4 + x³ + x² + 1=0
Eu comecei supondo que existe um número, racional escrito como uma fração irredutivel
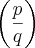
Dessa forma

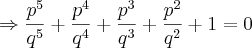
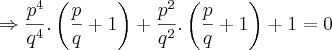

Mas daqui em diante eu não sei o que fazer e nem sei se estou no caminho certo!
Poderiam me ajudar
-
washington_araujo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jun 26, 2012 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM CIENCIA E TECNOLOGIA
- Andamento: cursando
 por e8group » Ter Jun 26, 2012 16:38
por e8group » Ter Jun 26, 2012 16:38
minha ideia foi essa :
1)

tais que
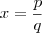
.
2) Seja

uma função ,onde
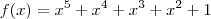
.
A parti de 1)Concluímos que


tal que

.
Prova :

.
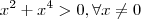
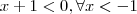
note que

Conclusão , como

,

tal que
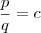
.
Espero que ajude ....
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Jun 27, 2012 23:23
por e8group » Qua Jun 27, 2012 23:23
Complementando a resolução ,até porque cometi erros no " Latex" ....
washington_araujo escreveu:Não existem soluções racionais para a equação x^5 + x^4 + x³ + x² + 1=0
Seja
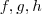
funções tais que

e
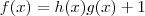
Pela definição de número racional sabemos que

tais que
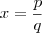
.
Vamos primeiro provar que existe um c tal que

,sabemos que c é ( real) entretanto ainda não sabemos se ele é ou não racional .
Prova :
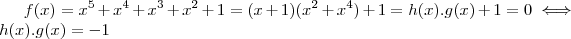
Como ,

e
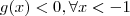
Então pelo fato de f ser contínua e " mudar de sinal " para
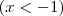
e
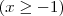
, veja ,por exemplo :
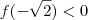
e
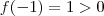
.Ou seja,como
![0 \in [f(-\sqrt{2},f(-1)] 0 \in [f(-\sqrt{2},f(-1)]](/latexrender/pictures/62e43d925b671c380d38577e9dc0ea15.png)
então

. (TVI ,veja :(
http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio ) ,assim concluímos que
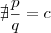
de modo que

tenha solução racional quando
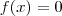
.
Há de ter uma resolução melhor !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por washington_araujo » Qui Jun 28, 2012 10:40
por washington_araujo » Qui Jun 28, 2012 10:40
SANTIAGO,
EU ENTENDI ATÉ A PARTE EM QUE A FUNÇÃO MUDA DE SINAL PARA (x<-1) E (x>1), MAS A PARTIR DO EXEMPLO EU NÃO ENTENDI COMO VOCÊ CHEGA A CONCLUSÃO, PODERIA EXPLICAR DE NOVO.
DESCULPA ESTAR PEDINDO MUITA EXPLICAÇÃO É QUE EU AINDA NÃO PEGUEI O JEITÃO DA COISA, MAS VALEU DESDE JÁ PELA RESOLUÇÃO JÁ ABRIU MUITO OS CAMINHOS PARA A RESOLUÇÃO DE ALGUNS OUTROS EXERCÍCIOS.
-
washington_araujo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jun 26, 2012 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM CIENCIA E TECNOLOGIA
- Andamento: cursando
 por e8group » Sex Jun 29, 2012 10:22
por e8group » Sex Jun 29, 2012 10:22
washington_araujo escreveu:EU ENTENDI ATÉ A PARTE EM QUE A FUNÇÃO MUDA DE SINAL PARA (x<-1) E (x>1), MAS A PARTIR DO EXEMPLO EU NÃO ENTENDI COMO VOCÊ CHEGA A CONCLUSÃO, PODERIA EXPLICAR DE NOVO.
washington araujo ,Vamos lá .
Primeiramente você sabe oque é função contínua , se não ! recomento a leitura do mesmo (
http://pt.wikipedia.org/wiki/Fun%C3%A7% ... t%C3%ADnua) .
" grosso modo " ...
o que eu fiz foi escolher valores a esquerda bem próximo de - 1 tais que c pertence a este intervalo .Note que
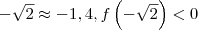
e
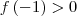
. Ou seja f " muda se sinal " orá positiva e negativa . Isso significa que
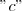
estar entre
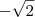
e

. Há um teorema muito legal que chama Teorema do valor Teorema do valor intermediário se você não conhece recomendo a leitura (
http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio) .
OBS .: Você consegue ver o gráfico de f no google ,basta pesquisar : x^5 + x^4 + x^3 + x^2 + 1
Abraços !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por washington_araujo » Sex Jun 29, 2012 11:33
por washington_araujo » Sex Jun 29, 2012 11:33
Muito obrigado santiago, valeu mesmo pela ajuda consegui compreender agora!!!
Abraços!
-
washington_araujo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jun 26, 2012 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: BACHARELADO EM CIENCIA E TECNOLOGIA
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova por redução ao absurdo
por Aliocha Karamazov » Sex Jun 10, 2011 21:34
- 1 Respostas
- 3310 Exibições
- Última mensagem por Guill

Sáb Jul 23, 2011 22:35
Álgebra Elementar
-
- Fazer a demonstração por absurdo
por apaula » Sex Fev 17, 2012 15:48
- 3 Respostas
- 2187 Exibições
- Última mensagem por MarceloFantini

Seg Fev 20, 2012 01:53
Álgebra Elementar
-
- PROVAR POR ABSURDO!!!!
por Rose » Sex Set 26, 2008 19:21
- 2 Respostas
- 3643 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:56
Geometria Plana
-
- Absurdo Matemático
 por PedroSantos » Sáb Jan 15, 2011 19:18
por PedroSantos » Sáb Jan 15, 2011 19:18
- 2 Respostas
- 1905 Exibições
- Última mensagem por PedroSantos

Dom Jan 16, 2011 19:42
Álgebra Elementar
-
- Deonstração por absurdo
por apaula » Sex Fev 17, 2012 12:04
- 2 Respostas
- 3841 Exibições
- Última mensagem por lua_guyl

Ter Jun 30, 2015 13:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
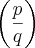

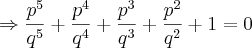
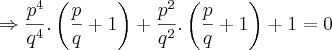


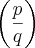

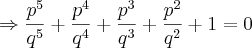
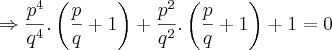


 tais que
tais que 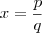 .
. uma função ,onde
uma função ,onde 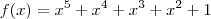 .
.
 tal que
tal que  .
. .
.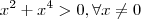
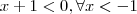

 ,
, tal que
tal que 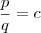 .
.
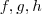 funções tais que
funções tais que  e
e 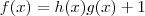
 tais que
tais que 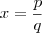 .
. ,sabemos que c é ( real) entretanto ainda não sabemos se ele é ou não racional .
,sabemos que c é ( real) entretanto ainda não sabemos se ele é ou não racional .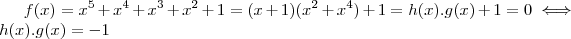
 e
e 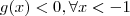
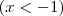 e
e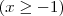 , veja ,por exemplo :
, veja ,por exemplo :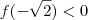 e
e 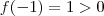 .Ou seja,como
.Ou seja,como ![0 \in [f(-\sqrt{2},f(-1)] 0 \in [f(-\sqrt{2},f(-1)]](/latexrender/pictures/62e43d925b671c380d38577e9dc0ea15.png) então
então  . (TVI ,veja :(http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio ) ,assim concluímos que
. (TVI ,veja :(http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio ) ,assim concluímos que 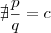 de modo que
de modo que  tenha solução racional quando
tenha solução racional quando 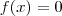 .
.

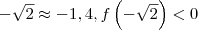 e
e 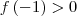 . Ou seja f " muda se sinal " orá positiva e negativa . Isso significa que
. Ou seja f " muda se sinal " orá positiva e negativa . Isso significa que 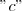 estar entre
estar entre 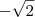 e
e  . Há um teorema muito legal que chama Teorema do valor Teorema do valor intermediário se você não conhece recomendo a leitura (http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio) .
. Há um teorema muito legal que chama Teorema do valor Teorema do valor intermediário se você não conhece recomendo a leitura (http://pt.wikipedia.org/wiki/Teorema_do ... i%C3%A1rio) .



 , avisa que eu resolvo.
, avisa que eu resolvo.

