Prove que
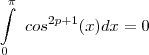 com p pertencente a Z.
com p pertencente a Z.(sugestão: faça
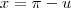 )
)eu tentei usar a sugestão e cai na mesma coisa de antes porém na variável u. Tentei dizer que u=senx e encontrei a seguinte integral:
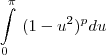
porém dai eu não consigo sair. Por favor, me ajudem!

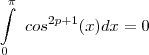 com p pertencente a Z.
com p pertencente a Z.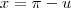 )
)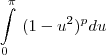

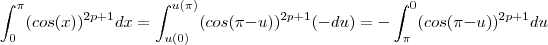 .
.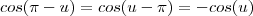 , temos , portanto
, temos , portanto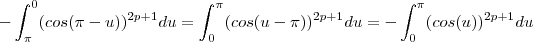 ,
,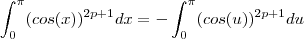 .
. e
e  são, nos processos de integração, variáveis "mudas", isto é, como efetua-se uma integração definida as variáveis, no resultado final, não aparecem explicitamente. Logo, podemos tomar
são, nos processos de integração, variáveis "mudas", isto é, como efetua-se uma integração definida as variáveis, no resultado final, não aparecem explicitamente. Logo, podemos tomar 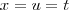 . Assim,
. Assim,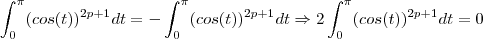 .
.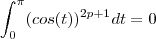

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)