 por citadp » Qua Jun 20, 2012 09:49
por citadp » Qua Jun 20, 2012 09:49
Tenho uma função x^6+3x^5 = -1
Pedem-me, mostre que a equação tem uma raiz em ]-1, 0 [
Ora, o que eu costumo fazer é derivar, o que me dá 6x^5+ 15x^4
Como não consigo calcular assim os zeros, simplifiquei : x^3(x^2 + 15x) = 0 o que me dá um zero em x=-15, o que supostamente me ensinaram foi que se a derivada não tiver zeros existe apenas um zero na função.
Assim a derivada tem zeros.
Alguém me pode ajudar a resolver isto ?
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Qua Jun 20, 2012 10:57
por e8group » Qua Jun 20, 2012 10:57
i) Teorema do valor intermediário :
OBS.: Note que
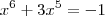
não é uma função ,é uma equação polinomial .
Mas seja uma função

,definida por
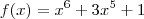
.
Como

é contínua (polinômio ) ,
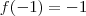
e

.
Como
![0 \in [ f(-1) ,f(0) ] = [ -1 ,1] 0 \in [ f(-1) ,f(0) ] = [ -1 ,1]](/latexrender/pictures/0feeb01495db72a6a828db9dfa53eeb7.png)
, pelo TVI existe um
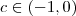
tal que
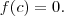
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por citadp » Qua Jun 20, 2012 11:24
por citadp » Qua Jun 20, 2012 11:24
Obrigada, já agora se fosse para igualar a zero, como calculava ?
Eu sei que existe a regra de ruffini, mas nunca sei qual o número que fica a multiplicar nestes casos.
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Qua Jun 20, 2012 11:38
por e8group » Qua Jun 20, 2012 11:38
citadp escreveu:Eu sei que existe a regra de ruffini, mas nunca sei qual o número que fica a multiplicar nestes casos.
Você pode utilizar o método de newton para aproximar raízes ,veja :
http://en.wikipedia.org/wiki/Newton%27s_method .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por citadp » Qua Jun 20, 2012 11:54
por citadp » Qua Jun 20, 2012 11:54
Outra questão, este exercicio diz também prove que a equação dada tem exactamente duas raízes reais.
Ora sem intervalo como provo isso ?
O que normalmente faria era derivar, calcular os zeros da derivada.
Após isso verificar se os zeros da derivada era zeros da função original e calcular também os zeros da função original num intervalo.
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida - Raízes
por hugo82 » Ter Mai 31, 2011 19:29
- 1 Respostas
- 1069 Exibições
- Última mensagem por Molina

Ter Mai 31, 2011 19:44
Álgebra Elementar
-
- Raízes dúvida
por LuizCarlos » Dom Mai 06, 2012 12:40
- 3 Respostas
- 1715 Exibições
- Última mensagem por DanielFerreira

Ter Mai 08, 2012 22:29
Álgebra Elementar
-
- [Função modular] Dúvida com relação a raízes
por exburro » Sáb Mar 31, 2012 01:23
- 1 Respostas
- 2590 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 12:40
Funções
-
- Dúvida em exercício - raízes de função quadrática
por Danilo » Qui Jun 07, 2012 01:50
- 1 Respostas
- 3185 Exibições
- Última mensagem por Russman

Qui Jun 07, 2012 03:32
Funções
-
- [DÚVIDA] Potências de expoentes racionais e raízes.
por invader_zim » Ter Fev 12, 2013 11:31
- 3 Respostas
- 2343 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 12:24
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


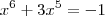 não é uma função ,é uma equação polinomial .
não é uma função ,é uma equação polinomial . ,definida por
,definida por 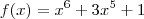 .
.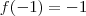 e
e  .
.![0 \in [ f(-1) ,f(0) ] = [ -1 ,1] 0 \in [ f(-1) ,f(0) ] = [ -1 ,1]](/latexrender/pictures/0feeb01495db72a6a828db9dfa53eeb7.png) , pelo TVI existe um
, pelo TVI existe um 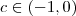 tal que
tal que 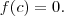


 .
.
 :
: