"Seja
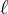 uma reta passando pelo ponto
uma reta passando pelo ponto  com inclinação negativa. Considere o triângulo retâgulo
com inclinação negativa. Considere o triângulo retâgulo  obtido tomando
obtido tomando  e BC o segmento da reta
e BC o segmento da reta 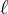 contido no primeiro quadrante. Ache as dimensões do triângulo
contido no primeiro quadrante. Ache as dimensões do triângulo  para que sua hipotenusa seja mínima"
para que sua hipotenusa seja mínima"Não estou conseguindo encontrar as relações e a função que tenho que derivar para aplicar o Teorema do Intervalo Fechado e o teste da primeira derivada...
Grato desde já!
.


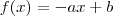 , onde
, onde  é uma constante positiva.
é uma constante positiva.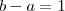 .
. e
e 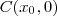 , tal que
, tal que 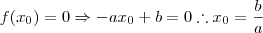 e
e 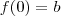 . Assim,
. Assim,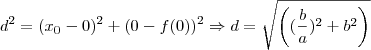 .
. se relacionam por
se relacionam por  na equação acima e teremos
na equação acima e teremos  , ou seja, a hipotenusa do triângulo unicamente como função de
, ou seja, a hipotenusa do triângulo unicamente como função de  .
. você precisa calcular que valor de
você precisa calcular que valor de  .
. precisamos que
precisamos que 
 não é válida pois de
não é válida pois de  chegamos em
chegamos em  oque é um absurdo, pois por hipótese
oque é um absurdo, pois por hipótese  .
. . Portanto, as dimensôes do triângulo são
. Portanto, as dimensôes do triângulo são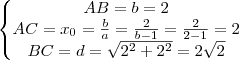


 .
.
 :
: