Dados os pontos A (a,0) e B (0,b), tomemos sobre a reta AB um ponto C de modo que BC = (m) x (AB) (m # 0 real). Pede-se a equação da reta perpendicular a AB, a qual passa pelo ponto médio do segmento AC.
Bom, a primeira coisa que fiz foi encontrar a equação da reta que passa por AB (reta que chamo de s) , que é b/ax- y - b. Sendo assim o coeficiente angular da reta que é perpendicular à reta s é -a/b. Bom, penso eu que agora só falta eu econtrar o ponto médio de AC. É aí que está o problema, não sei como encontrar... Sei que o ponto C está ''depois'' ou ''antes'' de AB pois BC = (m) x (AB) (m#0 real), me corrijam se eu estiver errado. Agradeço a qualquer ajuda. Valeu !


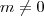 .
. . Além do sinal para y estar errado, você esqueceu de digitar "= 0" em sua "equação" (note que não podemos nem chamar de equação o que você escreveu, já que não tem uma igualdade!).
. Além do sinal para y estar errado, você esqueceu de digitar "= 0" em sua "equação" (note que não podemos nem chamar de equação o que você escreveu, já que não tem uma igualdade!).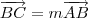 , temos que:
, temos que:




 .
.
 :
: