 por smlspirit » Sex Jun 15, 2012 01:42
por smlspirit » Sex Jun 15, 2012 01:42
Não consigo desenvolver o seguinte problema:
Dividindo um número de dois algarismo, cuja soma é 9, pelo quociente da divisão do algarismo das unidades pelo algarismo das dezenas, obtém-se o quociente 18. Qual é esse número?
Gostaria de uma ajuda para compreender o problema e montar a equação.
Obrigado
-
smlspirit
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mai 18, 2012 01:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: formado
 por Russman » Sex Jun 15, 2012 04:33
por Russman » Sex Jun 15, 2012 04:33
smlspirit escreveu:Não consigo desenvolver o seguinte problema:
Dividindo um número de dois algarismo, cuja soma é 9, pelo quociente da divisão do algarismo das unidades pelo algarismo das dezenas, obtém-se o quociente 18. Qual é esse número?
Gostaria de uma ajuda para compreender o problema e montar a equação.
Obrigado
Seja esse número

. Como ele tem apenas dois algarismos, sejam eles

e

, podemos escrever que
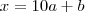
. Concorda?
Assim, vamos ao enunciado! Ele nos dá duas informações:
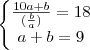
Eu acho interessante fato de que se a soma dos algarismos de um número é 9 então este é múltiplo de 9. Veja que isto nos dá apenas algumas combinações específicas para (a,b). Assim, podíamos fazer tentativas e verificar qual par satisfaz a equação 1. Maaaaaas, vamos recorrer a boa e confiável álgebra.
Da equação 1, podemos desenvolver que

.
Pela equação 2 sabemos que a e b se relacionam seguindo
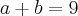
. Portanto, se tomarmos
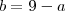
e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a!
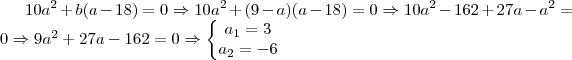
Como

deve ser um algarismo, a única solução válida é

. Agora, como eu sei que

é fácil imaginar que

, pelo argumento que eu dei acima. Claro,

.
Portanto, o seu número é 36!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- EQUAÇÕES FRACIONARIAS DO 2° GRAU [AJUDA URGENTE!!!]
por rayanne_ » Ter Mai 13, 2014 00:43
- 1 Respostas
- 1495 Exibições
- Última mensagem por Russman

Qua Mai 14, 2014 00:54
Equações
-
- [EQUAÇOES FRACIONARIAS] - AJUDA URGENTE!!
por mariaclarabg » Dom Set 09, 2012 20:39
- 2 Respostas
- 1417 Exibições
- Última mensagem por mariaclarabg

Dom Set 09, 2012 21:25
Equações
-
- [EQUAÇOES FRACIONARIAS] - agora de acordo com as regras
por mariaclarabg » Dom Set 09, 2012 21:24
- 2 Respostas
- 2412 Exibições
- Última mensagem por DanielFerreira

Seg Set 10, 2012 23:54
Equações
-
- equações de 2º grau
por Lismara » Seg Ago 31, 2009 23:25
- 4 Respostas
- 2836 Exibições
- Última mensagem por Lismara

Ter Set 01, 2009 21:42
Sistemas de Equações
-
- Equações 2º Grau
por Quatroemes » Dom Mar 21, 2010 20:53
- 2 Respostas
- 2611 Exibições
- Última mensagem por Quatroemes

Seg Mar 22, 2010 11:34
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Como ele tem apenas dois algarismos, sejam eles
. Como ele tem apenas dois algarismos, sejam eles  e
e  , podemos escrever que
, podemos escrever que 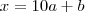 . Concorda?
. Concorda?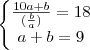
 .
.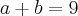 . Portanto, se tomarmos
. Portanto, se tomarmos 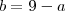 e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a!
e substituirmos na equação acima teremos uma equação de 2° grau na incógnita a! 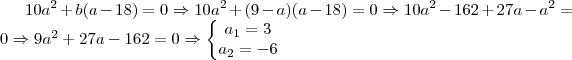
 . Agora, como eu sei que
. Agora, como eu sei que  é fácil imaginar que
é fácil imaginar que  , pelo argumento que eu dei acima. Claro,
, pelo argumento que eu dei acima. Claro,  .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.