juliacajango escreveu:oi pessoal, acabei de me registrar; tenho uma duvida em um exercicio da vunesp de domingo agora, dia 10/06/12, o enunciado diz :
Sabe-se que M, ponto médio do segmento AB, é centro de uma
circunferência que passa pela origem (0,0). Sendo A(–1,4) e
B(5,2), conclui-se que o raio dessa circunferência é igual a
tentei esboçar a figura, porém os pontos A e B não passam pelo centro no meu desenho, por favor, alguém sabe resolver este exercicio ?!
Como M é o ponto médio de AB, temos que:
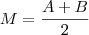

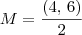
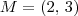
Como M é o centro da circunferência e O = (0, 0) é um ponto dessa circunferência, temos que o seu raio é equivalente a distância entre M e O. Temos então que:
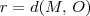
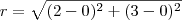
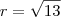
A figura abaixo ilustra o exercício.

- figura.png (11.78 KiB) Exibido 2623 vezes
Perceba que os pontos A e B ficarão dentro da circunferência. Isso irá acontecer pois o comprimento de AB é menor do que o diâmetro da circunferência. Confira isso! Calcule a distância entre A e B e você perceberá que ela é menor do que 2r.


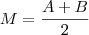

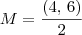
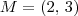
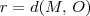
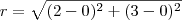
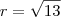

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.