Empacado numa das alternativas da questão. Fiz as 3 primeiras e empaquei na última. Vou postar todas as alternativas pois podem ser úteis na solução.
Dados P (2,2) e (r) 3x+2y-6 = 0, forneça:
a) equação de s perpendicular a r por P. (encontrei 2X-3Y+2=0)
b) o ponto M pé da perpendicular a r por P; (encontrei M (14/13, 10/13))
c) o ponto Q simétrico de P em relação a r; (encontrei Q ( 2/13, 10/13))
e que não estou conseguindo fazer...
d) a reta t simétrica de r em relação a P.
Bom, para resolver a d) utilizei os resultados anteriores que encontrei. Tracei, pelo ponto Q (2/13, 10/13) uma reta paralela à reta r. Como eu já sei a equação da reta r e esta reta r é perpendicular a r e a t, eu tenho o coeficiente angular de t e um ponto de t, logo eu tenho a equação da reta (me corrijam se eu estiver errado). aí, utilizei y-10/13= -3/2 ( x-2/13) => 3x-2y+2=0 cujo resultado não condiz com o correto segundo o livro, e no livro está 3x+2y+14=0. Agradeço qualquer ajuda, vlw!


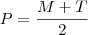 .
.