Me deparei com a seguinte questão: "Aplique os conceitos de integração para encontrar o volume de um tronco de cone circular reto de altura h, raio da base inferior R e raio de base superior r conforme ilustrado na figura abaixo:
Eu fiz umas relações forçadas, jogando a parte lateral triangular no eixo cartesiano, tentei também arrumar as relações por um trapézio, mas tudo me levou a uma resposta errada. Se alguém puder me ajudar, eu já agradeço a disposição. Toda ajuda é bem vinda.
O gabarito é:
(Bem prevísivel, não? huahua)Bem, eu voltei a tentar resolver essa questão, encontrei a seguinte relação entre os triângulos semelhantes pelas linhas que puxei dentro do próprio sólido, enfim, empaquei e nem sei se estar certo:
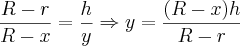
Logo, como a secção transversal é uma circunferência, temos que sua área é:
![A(x)=\pi\left[\frac{(R-x)h}{R-r}\right]^2](/latexrender/pictures/ecf9e586a072ae2ff9e5404985f6d7b6.png "A(x)=\pi\left[\frac{(R-x)h}{R-r}\right]^2")
E o volume do sólido é supostamente a seguinte integral:
![\int_{0}^{R}A(x) dx = \int_{0}^{R}\pi\left[\frac{(R-x)h}{R-r}\right]^2 dx](/latexrender/pictures/3fc302b50daf50ee5e5014fc3ea1d30c.png "\int_{0}^{R}A(x) dx = \int_{0}^{R}\pi\left[\frac{(R-x)h}{R-r}\right]^2 dx")
Bem, eu tentei resolver essa joça, mas ainda não está de acordo com o gabarito, portanto deixei assim mesmo... Pode ser que a relação esteja errada, mas eu creio que não. :/
Se estiver errado, não sei mais o que posso fazer.
OBS: Treco difícil, viu? (?°?°??? ???
.
![A(x) = \pi y^2 \implies A(x) = \pi \left[\dfrac{(h-x)(R-r)}{h} + r\right]^2](/latexrender/pictures/8e8d3c48600a8b1c2bef932eff137691.png "A(x) = \pi y^2 \implies A(x) = \pi \left[\dfrac{(h-x)(R-r)}{h} + r\right]^2")
![V = \int_0^h A(x) \,dx \implies V = \int_0^h \pi \left[\dfrac{(h-x)(R-r)}{h} + r\right]^2 \,dx](/latexrender/pictures/e6249ad9441a1025aa93b8bf9192c9f0.png "V = \int_0^h A(x) \,dx \implies V = \int_0^h \pi \left[\dfrac{(h-x)(R-r)}{h} + r\right]^2 \,dx")
por