 por gabriel17carmo » Sex Jun 08, 2012 23:16
por gabriel17carmo » Sex Jun 08, 2012 23:16
... formado pelos vetores:
V1 = (4, 2, -3)
V2 = (2, 1, -2)
V3 = (-2, -1, 0)
Olá, me deparei com esse exercício na minha apostila de gaal, porém não estou conseguindo resolver. Fiz a matriz com esses vetores e achei como solução {
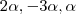
}, assim sendo, a base seria o vetor (2,-3, 1) e a dimensão seria 1, creio eu.
Mas no livro a dimensão do subespaço aparece como 2.
Alguém me explica no que estou errando, por favor?
Muito Grato
-
gabriel17carmo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 02, 2012 23:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por MarceloFantini » Sáb Jun 09, 2012 19:27
por MarceloFantini » Sáb Jun 09, 2012 19:27
Gabriel, antes de mais nada é necessário saber se o conjunto
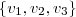
é linearmente independente. Você verificou isso? Se sim, não há mais o que fazer. Se não, quantos sobram?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gabriel17carmo » Sáb Jun 09, 2012 20:36
por gabriel17carmo » Sáb Jun 09, 2012 20:36
Verifiquei e vi que não é LI, pois tem duas linhas iguais e portanto o determinante é igual a 0.
Mas por que esse conjunto não pode ser LI? Achei que era a base que não poderia ser LI. :S
E não entendi quando você perguntou quantos sobraram.
Desculpe a ignorância.
-
gabriel17carmo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 02, 2012 23:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por gabriel17carmo » Sáb Jun 09, 2012 20:46
por gabriel17carmo » Sáb Jun 09, 2012 20:46
ahh acho que entendi. Esse conjunto de vetores v1, v2 e v3 seriam a base se fossem LI?
Aí eu vi que são LD, portanto um vetor é a combinação linear dos outros dois. Então eu posso pegar a base sendo o conjunto {v1, v2}, {v2, v3} ou até mesmo {v1, v3}?
Portanto se for qualquer uma dessas terá duas dimensões.
-
gabriel17carmo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 02, 2012 23:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por MarceloFantini » Sáb Jun 09, 2012 20:50
por MarceloFantini » Sáb Jun 09, 2012 20:50
Sim, exatamente. Se o conjunto
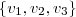
fosse LI, eles seriam a base. Você pode pegar como base quaisquer dois vetores que sejam linearmente independentes, se os conjuntos que você disse satisfazerem isto então está feito.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gabriel17carmo » Seg Jun 11, 2012 02:42
por gabriel17carmo » Seg Jun 11, 2012 02:42
Entendi, Muito Obrigado, foi de grande ajuda pra mim!
-
gabriel17carmo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 02, 2012 23:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra Linear]-Base e dimensão
por Ana_Rodrigues » Seg Mai 07, 2012 18:36
- 2 Respostas
- 3018 Exibições
- Última mensagem por Ana_Rodrigues

Ter Mai 08, 2012 23:12
Álgebra Linear
-
- algebra linear - base e dimensão do espaço de funçoes
por mou_duarte » Seg Mai 02, 2016 11:14
- 0 Respostas
- 1981 Exibições
- Última mensagem por mou_duarte

Seg Mai 02, 2016 11:14
Álgebra Linear
-
- Álgebra linear - Subespaço Gerado
por nietzsche » Sex Jan 06, 2012 19:48
- 2 Respostas
- 1909 Exibições
- Última mensagem por nietzsche

Ter Jan 10, 2012 17:16
Álgebra Linear
-
- [Álgebra Linear][Dúvida][Provar subespaço]
por Nicolas1Lane » Sex Set 12, 2014 16:45
- 1 Respostas
- 2100 Exibições
- Última mensagem por adauto martins

Qui Out 23, 2014 15:11
Álgebra Linear
-
- espaço linear -dimensão
por futuro fisico » Sáb Jul 02, 2011 17:23
- 3 Respostas
- 4125 Exibições
- Última mensagem por Renato_RJ

Dom Jul 03, 2011 17:13
Álgebra
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
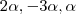 }, assim sendo, a base seria o vetor (2,-3, 1) e a dimensão seria 1, creio eu.
}, assim sendo, a base seria o vetor (2,-3, 1) e a dimensão seria 1, creio eu.

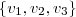 é linearmente independente. Você verificou isso? Se sim, não há mais o que fazer. Se não, quantos sobram?
é linearmente independente. Você verificou isso? Se sim, não há mais o que fazer. Se não, quantos sobram?
