 por Cleyson007 » Sáb Jun 09, 2012 16:24
por Cleyson007 » Sáb Jun 09, 2012 16:24
Calcule o limite:
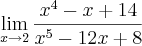
Estou resolvendo da seguinte forma:
f(2)= 28 e g(2)= 16
Para que as funções f e g sejam diferenciáveis devemos ter f(2) = g(2), correto?
f' (2)= 4x^3 -1 = 31
g' (2) = 5x^4 -12 = 68
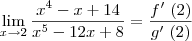
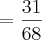
Está correta a resolução que apresentei?
Fico aguardando.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por joaofonseca » Sáb Jun 09, 2012 16:57
por joaofonseca » Sáb Jun 09, 2012 16:57
Se o objetivo é encontrar o limite da função quociente, nada mais simples que substituir
x por 2.Como não surge nenhuma indeterminação o limite será

.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Cleyson007 » Sáb Jun 09, 2012 19:50
por Cleyson007 » Sáb Jun 09, 2012 19:50
Boa noite João Fonseca!
Gostaria que comentasse a minha resolução para que eu entenda aonde estou errando..
Agradeço a ajuda.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Dom Jun 10, 2012 15:30
por MarceloFantini » Dom Jun 10, 2012 15:30
As funções

e

são diferenciáveis por serem polinômios. Seu argumento que devemos ter

é incorreto. Parece que você tentou aplicar L'Hospital e errou. Releia novamente as hipóteses e perceberá.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limite. Comecei estudar agora limites como resolvo isso?
por vinit » Ter Mar 12, 2013 12:26
- 1 Respostas
- 2278 Exibições
- Última mensagem por Douglas16

Ter Mar 12, 2013 14:40
Cálculo: Limites, Derivadas e Integrais
-
- Quebrando a cabeça ate agora :/
por Amandatkm » Dom Abr 28, 2013 17:48
- 8 Respostas
- 4190 Exibições
- Última mensagem por Amandatkm

Ter Abr 30, 2013 15:03
Equações
-
- [Algébra] Exercicios sem resultado, até agora.
por MatematicoRuim » Dom Mar 03, 2013 22:08
- 0 Respostas
- 1228 Exibições
- Última mensagem por MatematicoRuim

Dom Mar 03, 2013 22:08
Álgebra Elementar
-
- [EQUAÇOES FRACIONARIAS] - agora de acordo com as regras
por mariaclarabg » Dom Set 09, 2012 21:24
- 2 Respostas
- 2415 Exibições
- Última mensagem por DanielFerreira

Seg Set 10, 2012 23:54
Equações
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2786 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
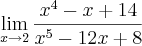
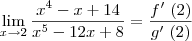
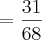

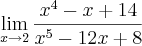
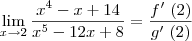
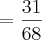

 .
.

 e
e  são diferenciáveis por serem polinômios. Seu argumento que devemos ter
são diferenciáveis por serem polinômios. Seu argumento que devemos ter  é incorreto. Parece que você tentou aplicar L'Hospital e errou. Releia novamente as hipóteses e perceberá.
é incorreto. Parece que você tentou aplicar L'Hospital e errou. Releia novamente as hipóteses e perceberá.
