Um vendedor propõe a um comprador de um determinado produto as seguintes alternativas de pagamento.
a) Pagamento à vista com 65 % de desconto sobre o preço da tabela.
b) Pagamento em 30 dias com desconto de 55 % sobre o preço de tabela.
Qual das duas alternativas é mais vantajosa para o comprador, considerando-se que ele consegue um rendimento de 25% com uma aplicação de 30 dias?
Resposta: Alternativa a)
Minha tentativa foi a seguinte:
Preço da tabela: x ----------- Vamos supor que o vendedor disponha de x
a) Pagando à vista
0,35x ( Vão sobrar 0,65x para o comprador)
b) Pagamento à prazo
Aplicando x, o rendimento será de: 1,25x
1,25x - 0,45x(Pagamento) = 0,8 x vão sobrar para o comprador
Logo, eu diria que o pagamento à prazo é mais vantajoso. Como vêem, pelo gabarito, me enganei. Alguém pode me indicar o jeito certo de fazer?


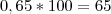 . Gastaria R$ 35,00.
. Gastaria R$ 35,00.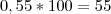 . Gastaria R$ 45,00.
. Gastaria R$ 45,00.
