 para que o SISTEMA tenha solução única:
para que o SISTEMA tenha solução única: = 4
= 4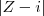 =
= 
Só consegui fazer que
 = x² + y² = 16 raio = 4
= x² + y² = 16 raio = 4 é uma equação da circunferência com raio = 4 ? Tenho que achar o afixo? como faço para achar o angulo?
Obrigada!!!!!!!

 para que o SISTEMA tenha solução única:
para que o SISTEMA tenha solução única: = 4
= 4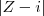 =
= 
 = x² + y² = 16 raio = 4
= x² + y² = 16 raio = 4 
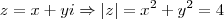


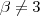 .
.
 e raio a determinar. Pela configuração do problema, vemos que a solução é
e raio a determinar. Pela configuração do problema, vemos que a solução é 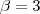 . Mas a circunferência pode tangenciar inferiormente apenas, logo
. Mas a circunferência pode tangenciar inferiormente apenas, logo 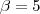 também.
também.


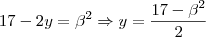 .
.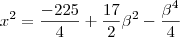
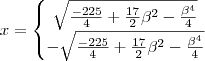
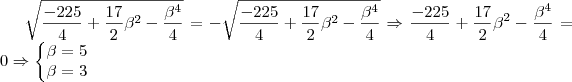 .
. , se
, se 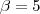 e
e 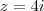 se
se 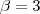 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes