 por amanda costa » Sex Jun 01, 2012 01:10
por amanda costa » Sex Jun 01, 2012 01:10
Teve uma questão na minha prova de cálculo hoje que gostaria de saber qual é a resposta certa
Na função

era pra mostrar se existia

eu calculei e deu -2, mas acho que está errada. Se alguém puder me mostrar como resolve eu agradeço.
-
amanda costa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 10, 2012 21:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sex Jun 01, 2012 01:46
por Russman » Sex Jun 01, 2012 01:46
O limite da derivada quando x tente a 0 pela esqerda é 2 e pela direita é -2. Logo, não existe o limite bilateral. Assim, a derivada não existe.
Desenvolvendo direitinho, eu sugiro que você tome a função definida para os reais positivos e negativos. Derive e então estude os limites para x tendendo a 0 pela direita e pela esquerda! Isto é,

Assim,
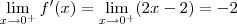
e
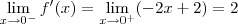
Como você vê o limite bilateral

,
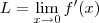
,
não existe. Assim, não existe a derivada dessa função em

.
Sinto muito.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Francisco de Brito » Sex Jun 01, 2012 11:02
por Francisco de Brito » Sex Jun 01, 2012 11:02
Uma função é derivável num ponto quando as derivadas laterais (a direita e a esquerda)
existem e são iguais neste ponto.
Só pra ter u,a noção melhor ainda do assunto .....
-
Francisco de Brito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 01, 2012 11:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por Francisco de Brito » Sex Jun 01, 2012 11:03
por Francisco de Brito » Sex Jun 01, 2012 11:03
Russman escreveu:O limite da derivada quando x tente a 0 pela esqerda é 2 e pela direita é -2. Logo, não existe o limite bilateral. Assim, a derivada não existe.
Desenvolvendo direitinho, eu sugiro que você tome a função definida para os reais positivos e negativos. Derive e então estude os limites para x tendendo a 0 pela direita e pela esquerda! Isto é,

Assim,
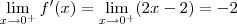
e
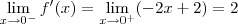
Como você vê o limite bilateral

,
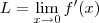
,
não existe. Assim, não existe a derivada dessa função em

.
Sinto muito.
Uma função é derivável num ponto quando as derivadas laterais (a direita e a esquerda)
existem e são iguais neste ponto.
-
Francisco de Brito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Jun 01, 2012 11:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
 por joaofonseca » Sex Jun 01, 2012 18:49
por joaofonseca » Sex Jun 01, 2012 18:49
Genericamente as funções modulo são continuas mas não são difererenciáveis
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivar a função
por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
- 3 Respostas
- 3852 Exibições
- Última mensagem por SILMARAKNETSCH

Qua Nov 14, 2012 21:57
Funções
-
- Derivar uma função
por rcs01 » Qui Abr 30, 2015 09:48
- 0 Respostas
- 2344 Exibições
- Última mensagem por rcs01

Qui Abr 30, 2015 09:48
Cálculo: Limites, Derivadas e Integrais
-
- Derivar utilizando a de função ?
por Charlys Couto » Sex Abr 29, 2011 12:19
- 5 Respostas
- 3581 Exibições
- Última mensagem por Yokotoyota

Qui Fev 04, 2016 04:46
Cálculo: Limites, Derivadas e Integrais
-
- Como derivar esta função: (x^3 + 7x^2 -8).(2x^-3 + x^-4)
 por fabio carvalho » Dom Mai 29, 2016 01:50
por fabio carvalho » Dom Mai 29, 2016 01:50
- 1 Respostas
- 2791 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 21:43
Cálculo: Limites, Derivadas e Integrais
-
- quais os Passos para derivar essa função
por Netolucena » Seg Nov 05, 2012 20:43
- 2 Respostas
- 8780 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 21:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 era pra mostrar se existia
era pra mostrar se existia 

 era pra mostrar se existia
era pra mostrar se existia 


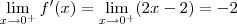
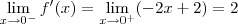
 ,
,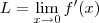 ,
, .
.

,
,
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.