No retângulo LUAR, a medida de RL é o dobro da medida de AR.
Para que medidas do lado RL, de LUAR, a área de LEAR será maior que
 .
.Tentei resolver dessa forma:
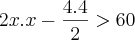

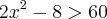

Mas a resposta não é essa, o gabarito é

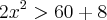
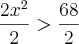
Olá amigo djr, esqueci de anexar a figura do retângulo!




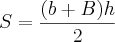
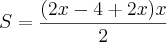
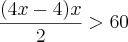
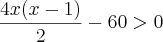

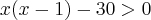




 .
.
 :
: