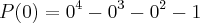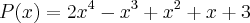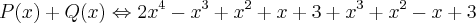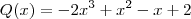Não consigo entender os seguientes tipos de exercicios, segue:
1) Dê o grau dos Polinômios
P(X)= 5x²-3x-2
Segundo a apostila a resposta dessa é : 2
2) Dado o polinômio P(X)= x(ao quarto)+x³-x²-1. calculo o P(0):
A Respota segundo o livro é: -1
Eu gostaria de saber como resolvo esse tipo de exercicios? a resposta para mim não é importante pois já a tenho eu quero saber como faço para chegar até ela, preciso aprender essa matéria! obrigado pela força!



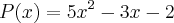
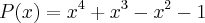
 , temos:
, temos: