Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
desde de já agradeço.



edu2012 escreveu:Boa tarde, gostaria de um exemplo de integral imprópria quando ela converge ou Diverge até agora não estou entendendo.
um exemplo
?
? x+1/(x²+2x) dx
1
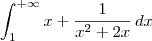
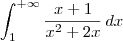
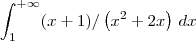
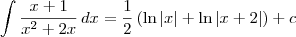
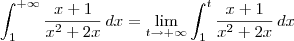
![= \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t = \lim_{t\to+\infty} \left[\frac{1}{2}\left(\ln|x| + \ln|x+2|\right)\right]_1^t](/latexrender/pictures/5254ecef9540c8883a9438aca418ea60.png)
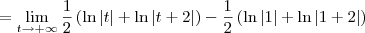
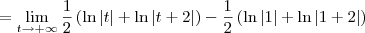
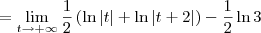
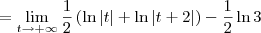
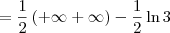

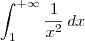
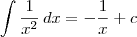
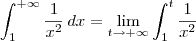
![= \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t = \lim_{t\to +\infty} \left[-\frac{1}{x}\right]_1^t](/latexrender/pictures/765779293a3854676a11157002910beb.png)
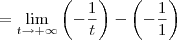


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

