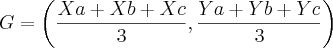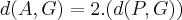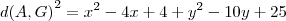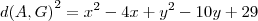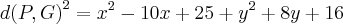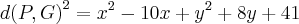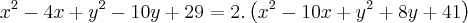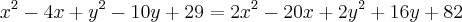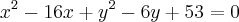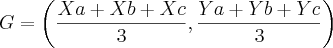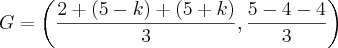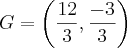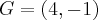por Matheus Lacombe O » Dom Mai 27, 2012 18:49
por Matheus Lacombe O » Dom Mai 27, 2012 18:49
Cálculo de Baricentro com um vértice e um ponto médio- Olá pessoal. Continuo resolvendo a minha antiga apostila positivo e heis que me surge outra dúvida.
- No enunciado deste problema tenho apenas dois pontos de um triangulo ABC. Sendo eles, um vértice A(2,5) e o ponto médio entre os vértices 'B' e 'C' - que chamei de P(5,-4). Com apenas estes dois dados o enunciado pede que seja calculado "[..]o ponto de intersecção das medianas do triângulo ABC.", ou seja, as coordenadas do baricentro
Tentativas:- Bem, antes de mostrar os cálculos gostaria de expor o raciocíneo. Como não tenho os pontos 'B' e 'C' acho que é impossível calcular o baricentro pela fórmula abaixo:
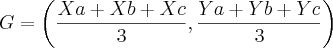
- Portanto, tentei resolver usando a razão de 2/1, uma vez que o baricentro (G) divide as medianas na razão de dois para um.
 - Logo:
- Logo: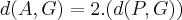 - Calculando a distancia AG
- Calculando a distancia AG
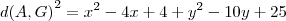
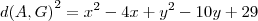 - Calculando a distancia PG:
- Calculando a distancia PG:
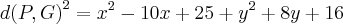
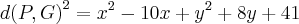 - Se d(A,G) = 2.(d(P,G)), logo:
- Se d(A,G) = 2.(d(P,G)), logo: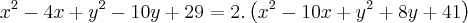
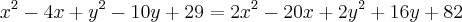
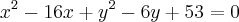 - E agora? não chego a lugar algum!
- E agora? não chego a lugar algum!
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 21:24
por DanielFerreira » Dom Mai 27, 2012 21:24
Matheus,
não garanto que meus cálculos estejam corretos. Fiz assim:
Considerando P o ponto médio de BC (supondo B à esquerda de P), digamos que o segmento BC = 2k, temos que:
B = (5 - k, - 4) e C = (5 + k, - 4)
Com isso:
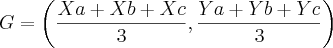
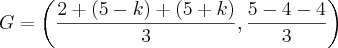
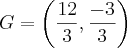
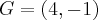
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida - ponto medio e coordenada
por deividchou » Qua Ago 07, 2013 13:55
- 2 Respostas
- 1616 Exibições
- Última mensagem por deividchou

Qua Ago 07, 2013 19:04
Geometria Analítica
-
- Área - Sejam ABCD um quadrado de lado 12 cm, E o ponto médio
por marguiene » Sex Out 10, 2014 10:40
- 0 Respostas
- 1573 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:40
Geometria Plana
-
- Cálculo de preço médio de custo
por danniyolivas » Qua Jul 08, 2015 11:53
- 1 Respostas
- 2003 Exibições
- Última mensagem por danniyolivas

Dom Jul 12, 2015 06:54
Matemática Financeira
-
- Cálculo, Valor Médio. Velocidade instantânea.
por leocastilho » Qua Jun 12, 2013 12:35
- 1 Respostas
- 1639 Exibições
- Última mensagem por e8group

Qua Jun 12, 2013 22:40
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de um ponto do paralelogramo
por jmcustodio » Dom Set 30, 2012 23:46
- 1 Respostas
- 1356 Exibições
- Última mensagem por young_jedi

Dom Set 30, 2012 23:59
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.