 por brunock » Ter Mai 22, 2012 16:14
por brunock » Ter Mai 22, 2012 16:14
Olá gente, tudo bem?
Sou novo aqui no Fórum, e gostaria de saber se vocês poderiam me ajudar em alguns exercícios com Regra de Cramer.
Estou com dificuldades, pois perdi a explicação do professor e agora não consigo desenvolver os exercícios passados... Poderiam me ajudar? Aqui estão eles:
a) { x + y = 6
x - y = 2
b) { 2x + 4 y = 3
3x - 2 y = 1
c) { x - y + Z = 0
x + 2y - 2Z = 3
2x - y - Z = -3
d) { x - y + Z = 0
2x - 4y + 6Z = 1
x + y + Z = 3
Até onde sei, é necessário passar essas dados para um determinante, mas como funciona essa montagem? Eu li alguns exemplos na internet mas não consegui compreender...
Desde já muitíssimo obrigado!
-
brunock
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 22, 2012 16:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 15:04
por DanielFerreira » Dom Mai 27, 2012 15:04
a)
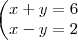
Calculando

:

Calculando

:

Calculando
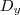
:

Obtemos x efetuando a divisão
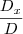
, veja:
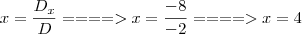
Obtemos y efetuando a divisão

:

Note que, para calcular

coloquei na primeira coluna (coeficientes de x) os termos independentes das equações.
Para calcular
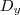
, ponha os termos independentes das equações na segunda coluna (coeficientes de y).
Tente fazer a "b", caso não consiga exponha as dúvidas!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes] Regra de Cramer
por jessica cheang » Ter Jun 09, 2015 19:13
- 0 Respostas
- 3699 Exibições
- Última mensagem por jessica cheang

Ter Jun 09, 2015 19:13
Matrizes e Determinantes
-
- Função (Precisando urgentemente me encontrar neste assunto)
por adna » Qui Fev 20, 2014 00:11
- 3 Respostas
- 2277 Exibições
- Última mensagem por Russman

Seg Fev 24, 2014 00:10
Funções
-
- escalonamento e não Cramer :s
por Sofiaxavier » Sáb Nov 20, 2010 15:19
- 4 Respostas
- 3007 Exibições
- Última mensagem por Molina

Dom Nov 21, 2010 19:20
Matrizes e Determinantes
-
- Método de Cramer
por Stephani » Dom Mai 24, 2015 16:07
- 3 Respostas
- 10579 Exibições
- Última mensagem por Cleyson007

Dom Mai 24, 2015 18:01
Matrizes e Determinantes
-
- [Ajuda] Regra de Simpson
por kaaps » Sáb Mai 12, 2012 20:54
- 1 Respostas
- 1906 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 09:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


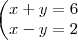
 :
:
 :
:
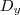 :
:
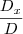 , veja:
, veja: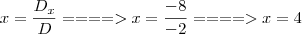
 :
:

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.