 por Larice Mourao » Dom Mai 27, 2012 02:01
por Larice Mourao » Dom Mai 27, 2012 02:01
Bem , pode até ser uma pergunta bestinha , mas quando tento encontrar um par ordenado a partir de uma equação da reta , seja reduzida ou geral , eu acabo indo por tentativas . Tipo : 2x+y=0 eu encontro valores que substituem as variáveis e calculando dê 0. Eu procurei na internet .. mas não vi algo mais específico , a não ser para retas concorrentes que fazendo um Sistema dá pra encontrar o X e o Y (par ordenado)... então , tem alguma formula de encontrar sem ser por tentativas ou lógica ?
Aqui : Qual a área do paralelogramo definido pelas retas y=2x, y=2x+2, x=0 e x=2?
Fiz assim: montei no plano cartesiano um vértice em (0,0) e outro com (2,0) , o resto não consegui .. alguém pode me ajudar a encontrar o par ordenado aí dá pra achar a área: b.h
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Mai 27, 2012 13:38
por DanielFerreira » Dom Mai 27, 2012 13:38
Larice,
nesse caso, deverá esboçar as retas

e
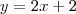
e marcar os pontos (0,0) e (2,0).
Através dos pontos, observe que x varia de 0 à 2; com isso, basta calcular o valor que y assumirá naquele intervalo.
Reta y = 2x:
=> quando x = 0
y = 2.0
y = 0(0,0)=> quando x = 2
y = 2.2
y = 4(2,4)Reta y = 2x + 2:
=> quando x = 0
y = 2.0 + 2
y = 2(0,2)=> quando x = 2
y = 2.2 + 2
y = 6(2,6)Espere ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Larice Mourao » Seg Mai 28, 2012 23:33
por Larice Mourao » Seg Mai 28, 2012 23:33
Olá .. se não for pedir mt e só para confirmar .. a a área é 4 ? e pra encontrar uma reta , portanto , é só substituir os pontos que limitam a reta ?
Muito obrigada, ajudou muitíssimo !!


-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qui Mai 31, 2012 22:55
por DanielFerreira » Qui Mai 31, 2012 22:55
Larice,
fique à vontade e pode perguntar.
(...) e pra encontrar uma reta , portanto , é só substituir os pontos que limitam a reta ?
Uma reta tem infinitos pontos, então, para esboçá-la vc deve atribuir valores (quaisquer) a
x, dessa forma irá obter
y.
Vou te dar outra dica:
==> Esboce a reta y = 2x;
==> Esboce a reta y = 2x + 2;
==> Esboce a reta x = 0;
==> Esboce a reta x = 2.
Mostre como encontrou
4.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Larice Mourao » Qui Mai 31, 2012 23:20
por Larice Mourao » Qui Mai 31, 2012 23:20
então .. ainda não sei desenhar em latex um plano cartesiano - desculpe-me .
Mas vou tentar explicar : Como vc demonstrou _ na 1ª resposta _ como se encontra os pontos das duas retas eu marquei , para a reta y=2x (0,0) , um ponto na origem; o outro par (2,4) um ponto com 2 no eixo das abcissas e 4 no da ordenada aí tracei a reta entre esses pontos .
Depois fiz o mesmo para y=2x+2 : um ponto _ (0,2) _ com apenas o 2 na ordenada; e o outro ponto _ (2,6) _ o 2 na abcissa e 6 no eixo das ordenadas e tracei a reta entre esses pontos ..
Daí , a figura é um paralelogramo .
A altura é 2 , diferença entre o 6 e 4 da ordenada ou o 2 e 0
e a base é 2 , diferença entre o 2 e 0 nas abcissas .
Logo , A= b . h
A= 2 . 2 = 4
ufa ! rsrs .. fiz assim

..
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Jun 03, 2012 17:01
por DanielFerreira » Dom Jun 03, 2012 17:01
Olá
Larice,
boa tarde!!
Desenhou corretamente a figura. No entanto, não pode concluir que a base vale 2, veja:
Vamos 'nomear' os pontos, para que possa entender melhor!
Considere:
(0,0) =

(2,0) =

(2,4) =

Presumo que
AC seja o que vc está consirando como base, certo?!
ABC é um triângulo retângulo, onde AB = 2, BC = 4 e AC = ?
Dica:
Encontre
AC aplicando o Teorema de Pitágoras e obtenha o resultado multiplicando
AC pela altura
Larice escreveu:A altura é 2 , diferença entre o 6 e 4 da ordenada ou o 2 e 0
Encontrei

.
Qualquer dúvida, retorne!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Larice Mourao » Qui Jun 07, 2012 23:39
por Larice Mourao » Qui Jun 07, 2012 23:39
hihi , mas com aqueles pares ordenados ficou um paralelogramo .. não visualizei nenhum triangulo ..... por que vc desconsiderou os outros pares .. ?
Boa noite !
-
Larice Mourao
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 17, 2012 15:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Encontrar equação (vetorial) da reta
por elisafrombrazil » Qua Abr 19, 2017 21:52
- 0 Respostas
- 1820 Exibições
- Última mensagem por elisafrombrazil

Qua Abr 19, 2017 21:52
Álgebra Linear
-
- [Derivadas] Encontrar a equação da reta tangente
por MrJuniorFerr » Qua Out 17, 2012 12:01
- 1 Respostas
- 2279 Exibições
- Última mensagem por MarceloFantini

Qua Out 17, 2012 12:21
Cálculo: Limites, Derivadas e Integrais
-
- Encontrar formula a partir de um intervalo
por leonardooliv » Sex Jun 23, 2017 10:12
- 0 Respostas
- 1587 Exibições
- Última mensagem por leonardooliv

Sex Jun 23, 2017 10:12
Funções
-
- [Geometria Analítica] Encontrar a reta t
por -civil- » Ter Ago 09, 2011 21:49
- 1 Respostas
- 2206 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 23:31
Geometria Analítica
-
- encontrar a inclinacção da reta tangenti
por elizeu » Seg Mai 21, 2012 13:25
- 1 Respostas
- 1044 Exibições
- Última mensagem por LuizAquino

Ter Mai 22, 2012 14:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 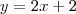 e marcar os pontos (0,0) e (2,0).
e marcar os pontos (0,0) e (2,0).


 ..
..


 .
.