
Só pra explicar: não prestei o concurso, mas fiquei bastante curiosa em relação à resolução desta questão. Alguém gostaria de opinar?
(CESPE/ANAC/ 2009/Cargo 6: Analista Administrativo – Área 1)
Em um voo em que haja 8 lugares disponíveis e 12 pessoas que desejem embarcar, o número de maneiras distintas de ocupação dos assentos para o voo sair lotado será superior a 500. (V ou F?)
Antes de mostrar o gabarito .... fiquei pensando qual fórmula aplicar:
1) Arranjo? faz sentido, pois os lugares em avião são diferentes: janela/corredor- me fez pensar que a *ordem é importante*, maneiras distintas.
A (12,8) =

2) Combinação? faz sentido se vc pensar que vai pescar indistintamente 8 pessoas entre as 12, mas acho que não justifica a ocupação dos assentos.
C (12,8) =
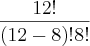
3) Permutação? Até nisso pensei... afinal, a questão diz *maneiras distintas de ocupação dos assentos* então, a partir dos já selecionados 8 em 12... quem vai ocupar qual lugar, sugere uma permutação.
P (8) = 8!
4) C +A : Considerando que, a forma de escolher quem vai entrar no voo não é importante, mas ocupar os assentos importa e não pode ser indistinta.
C (12,8) x A (8,1) =
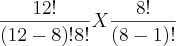
O fato é que ... a resposta é E (falso!) Fiquei surpresa, pois para qualquer destes raciocínios o resultado é superior a 500, exceto o de nr. 2 . O que vcx acham???
Obrigada! Roberta

Obs... o gabarito ainda é o preliminar.



 Obrigada!!
Obrigada!!![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)